Lektion G29: Biquadratische Gleichungen
Quartische Gleichungen sind Gleichungen 4. Grades. Fehlen x³ und x in der Gleichung, so sprechen wir von biquadratischen Gleichungen.
Diese biquadratischen Gleichungen können wir mit Hilfe der Substitution lösen. Die Substitution bringt die Gleichung 4. Grades auf eine Gleichung 2. Grades, die sich dann mit den bekannten Lösungsverfahren für quadratische Gleichungen berechnen lässt.
Zusätzlich erklären wir im zweiten Video, mit welchen weiteren Lösungsverfahren wir reduzierte quartische Gleichungen lösen können.
Weitere Videos für Kunden:
-
G29-1 Biquadratische Gleichungen - SubstitutionÜbersicht zu Gleichungen 1. bis 3. Grades. Was sind biquadratische Gleichungen und wie können wir diese mit Hilfe der Substitution (Ersetzung) berechnen. Lösung am Beispiel: -0,5·x⁴ + 4·x² - 3,5 = 0.
-
G29-2 Biquadratische Gleichungen - Quartische GleichungenWir lösen reduzierte Quartische Gleichungen (4. Grad) mit Wurzelziehen, Ausklammern und Satz vom Nullprodukt. Lösung als Nullstellen von Funktionsgraphen. Zusammenfassung der Lösungsverfahren für die Gleichungstypen. Lösen einer Gleichung 6. Grades per Substitution.
Nachdem ihr die Unbekannten einer Gleichung substituiert habt und nur noch eine quadratische Gleichung vorliegt, könnt ihr das folgende Programm nutzen, um die Lösungen zu bestimmen.
-
 Quadratische Gleichungen und p-q-FormelDieses Programm löst beliebige quadratische Gleichungen mit Hilfe der p-q-Formel, inklusive Rechenweg.
Quadratische Gleichungen und p-q-FormelDieses Programm löst beliebige quadratische Gleichungen mit Hilfe der p-q-Formel, inklusive Rechenweg. -
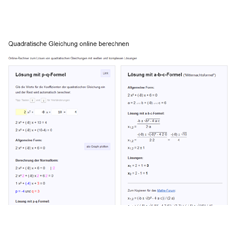 Quadratische Gleichung RechnerDie Lösung wird euch komplett mit Rechenweg angezeigt. Zum einen mit p-q-Formel und zum anderen mit abc-Formel, sog. Mitternachtsformel.
Quadratische Gleichung RechnerDie Lösung wird euch komplett mit Rechenweg angezeigt. Zum einen mit p-q-Formel und zum anderen mit abc-Formel, sog. Mitternachtsformel.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 4 Lernchecks, mit denen du dein Wissen testen kannst.


