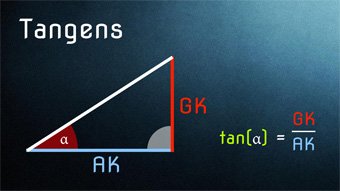
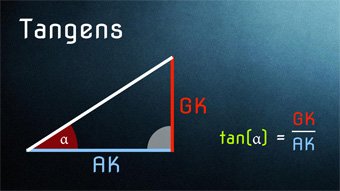
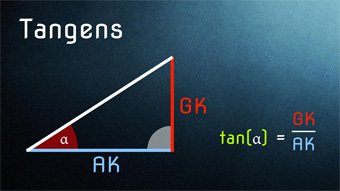
Lektion TRI04: Tangens
Nach Sinus und Kosinus folgt nun der Tangens, also das Verhältnis aus Gegenkathete und Ankathete. Was das genau bedeutet, erfahrt ihr in den Mathe-Videos.
Weitere Videos für Kunden:
-
TRI04-1 Tangens - Einfache EinführungWas ist der Tangens, wie ist er definiert. Was bedeutet das Seitenverhältnis Gegenkathete zu Ankathete. Anwendung des Tangens zur Seitenbestimmung und Anwendung des Arkustangens zur Winkelbestimmung.
-
TRI04-2 Tangens - Tangens für Winkel von 0° bis 180°Tangens von 0° bis 180° im Koordinatensystem ablesen, besondere Tangenswerte für 0°, 90° und 180°. Negativer Tangens. Tangens als Steigung. Ermittlung der Steigung einer linearen Funktion mit Hilfe des Tangens.
-
TRI04-3 Tangens - Zusammenfassung + Aufgaben lösenZusammenfassung des neuen Wissens. Tangens als Sinus/Kosinus. Aufgaben: Höhenbestimmung aus Winkel und Distanz. Winkelbestimmung aus Höhe und Distanz. Wann nutzt man Sinus, Kosinus oder Tangens.
-
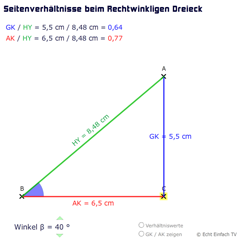 Sinus und Kosinus: SeitenverhältnisseSeht hier die Seitenverhältnisse beim rechtwinkligen Dreieck, die zu Sinus und Kosinus führen. Sinus als Verhältniswert von Gegenkathete/Hypotenuse und Kosinus als Ankathete/Hypotenuse.
Sinus und Kosinus: SeitenverhältnisseSeht hier die Seitenverhältnisse beim rechtwinkligen Dreieck, die zu Sinus und Kosinus führen. Sinus als Verhältniswert von Gegenkathete/Hypotenuse und Kosinus als Ankathete/Hypotenuse. -
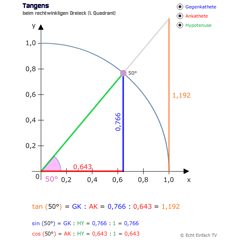 Tangens beim rechtwinkligen DreieckEntdeckt hier die Tangens-Werte für Winkel von 0° bis 90°. Der Tangens ergibt sich aus Gegenkathete durch Ankathete aber auch aus dem Verhältnis Sinus durch Kosinus.
Tangens beim rechtwinkligen DreieckEntdeckt hier die Tangens-Werte für Winkel von 0° bis 90°. Der Tangens ergibt sich aus Gegenkathete durch Ankathete aber auch aus dem Verhältnis Sinus durch Kosinus. -
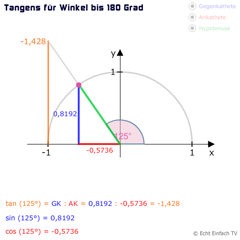 Tangens für Winkel bis 180 GradBei diesem Programm werden die Werte für Sinus, Kosinus und Tangens für Winkel von 0° bis 180° angezeigt. Kosinus und Tangens sind bei Winkeln zwischen 90° und 180° negativ!
Tangens für Winkel bis 180 GradBei diesem Programm werden die Werte für Sinus, Kosinus und Tangens für Winkel von 0° bis 180° angezeigt. Kosinus und Tangens sind bei Winkeln zwischen 90° und 180° negativ!
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Tangens - Einführung
- Mögliche Tangenswerte
- Tangens als Verhältnis von Sinus / Kosinus
- Tangens in den Taschenrechner eingeben
- Arkustangens: Winkel aus Tangenswert berechnen
- Dreiecksseiten mit Tangens bestimmen
- Tangens am Dreieck ablesen
- Steigung einer linearen Funktion mit Tangens berechnen
- Steigungswinkel mit Arkustangens bestimmen
- Tangens Wortherkunft
- Tangenswerte für Winkel von 90° bis 180°
- Sinus, Kosinus oder Tangens anwenden?
- Tangenswerte größer 1 und kleiner -1
- Tangenstabelle von 0° bis 180°