Wir haben bereits Zahlenstrahlen kennengelernt, auf denen wir natürliche Zahlen eingetragen haben.
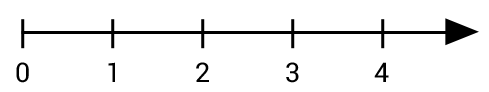
Wenn wir nun jedoch eine Zahl zwischen 1 und 2 suchen, welche Zahl wäre das dann?
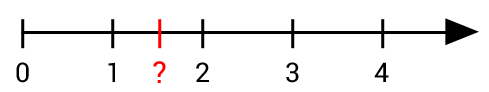
Um diese Zahl zu bestimmen, verwenden wir die sogenannte Kommaschreibweise.
Wir setzen ein Komma (das ist ein kleiner Strich ,) hinter die natürliche Zahl 1 und schaffen auf diese Weise eine weitere Stelle (1,_).
Damit können wir die folgenden neuen Zahlen (sogenannte „Kommazahlen“) schreiben:
1,1 1,2 1,3 1,4 1,5
1,6 1,7 1,8 1,9.
Wir können uns diese Kommazahlen auch am Zahlenstrahl vorstellen. Hierzu vergrößern wir den Zahlenstrahl und betrachten den Bereich zwischen 1 und 2. Zudem unterteilen wir die Strecke zwischen 1 und 2 wie folgt:
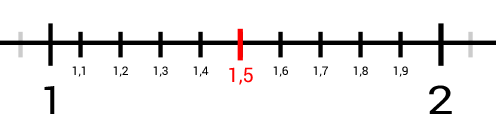
Wie wir sehen, ist die gesuchte Zahl die 1,5.
Das heißt, 1,5 liegt genau in der Mitte zwischen 1 und 2.
Übrigens können wir die 1 auch schreiben als 1,0 sowie die 2 als 2,0.
Die Kommazahlen von 1,0 bis 2,0 lauten also:
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
