In der Abbildung sehen wir den Sinusgraph (rötlich) und den Kosekansgraph (blau):
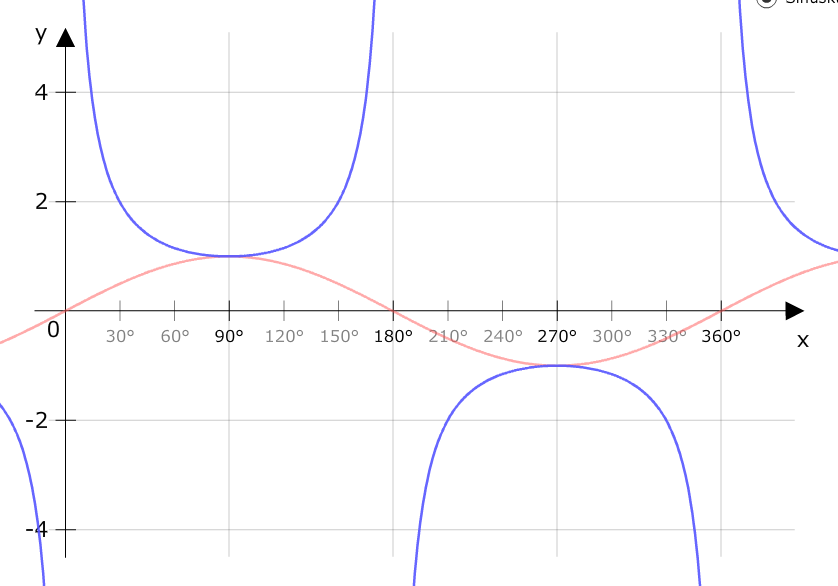
Jeder einzelne Wert der Sinusfunktion wird durch 1 gerechnet und wir erhalten diesen blauen Graphen. Bei 90° haben Sinusfunktion und Kosekansfunktion den gleichen Wert 1, denn sin(90°) = 1 und csc(90°) = 1⁄1 = 1.
Und hier sehen wir auch, dass kein Wert der Kosekansfunktion kleiner als 1 sein darf, denn die Hypotenuse kann ja nicht kürzer als die Gegenkathete sein.
Die Periode ist bei beiden Graphen gleich mit 0° bis 360°. Wo der Sinus 0 ist, ist der Kosekans nicht definiert, also zum Beispiel bei 0° und 180°. Dort haben wir sogenannte Definitionslücken.
Wie bei der Sinusfunktion können wir auch bei Kosekansfunktion die Periode verändern, den Graphen nach oben und nach unten verschieben, nach links und rechts verschieben, stauchen und strecken - und schließlich Berechnungen anstellen.
Beispiel eines veränderten Kosekansgraphen:
~plot~ csc(x);4*sec(x+pi);zoom[[10]];noinput ~plot~