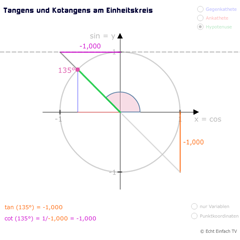
Der Kotangens lässt sich im Einheitskreis ebenfalls ablesen, siehe lila gefärbte Linie:
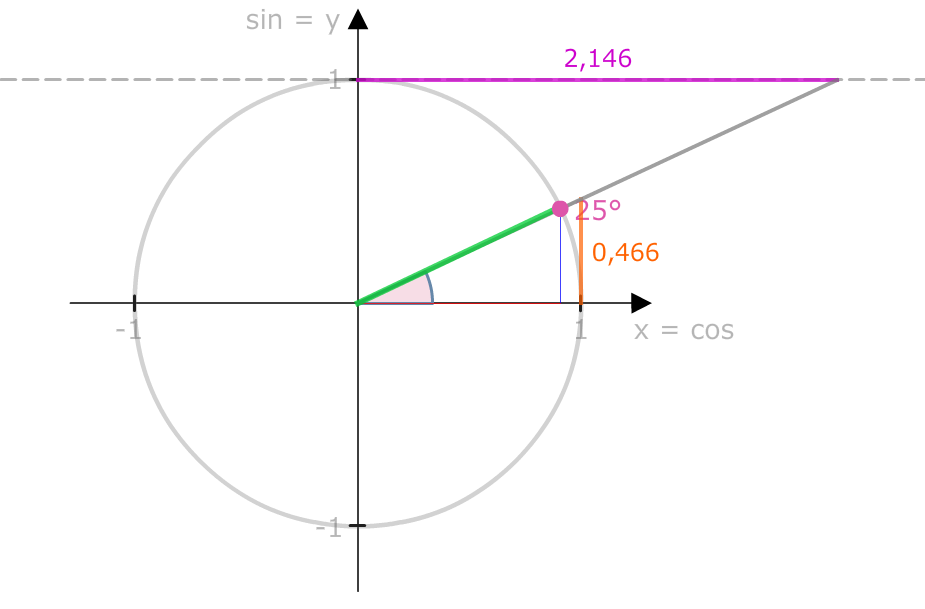
Warum ist dies möglich? Zeigen wir das, indem wir ein rechtwinkliges Dreieck einsetzen:
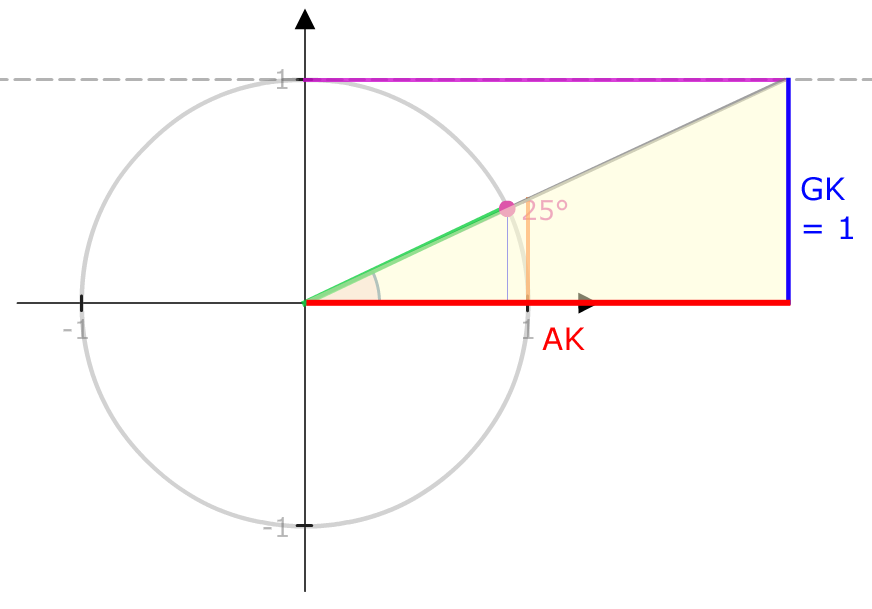
Wir sehen, dass die Gegenkathete immer 1 lang ist. Der Tangens ist also:
tan(α) = \( \frac{GK}{AK} \)
tan(α) = \( \frac{1}{AK} \) | · AK
tan(α) · AK = 1 | : tan(α)
AK = \( \frac{1}{\tan(α)} \)
Die Ankathete ist \( \frac{1}{\tan(α)} \) lang, was dem Kotangens entspricht.