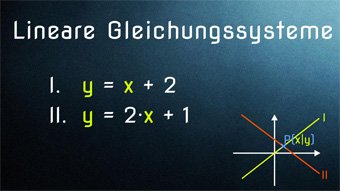Lektion F06: Lineare Gleichungssysteme
Eine Abkürzung, auf die man im Mathematik-Unterricht oft stößt, ist „LGS“. „LGS“ steht für Lineares Gleichungs-System. Damit ist allgemein das Lösen von linearen Gleichungen gemeint, die in Verbindung gebracht werden und dadurch im Normalfall nur eine Lösung für x und y haben.
Im ersten Video zeigen wir euch in Kürze wie man ein Lineares Gleichungssystem löst, das aus zwei Gleichungen besteht. Wir schauen uns dazu drei Verfahren an: Gleichsetzungsverfahren | Einsetzungsverfahren | Additionsverfahren.
In den Videos 2 bis 5 wird das Lösen von linearen Gleichungssystemen mit Funktionen veranschaulicht. Hier ist es notwendig, dass ihr die Lektion Schnittpunkt von zwei linearen Graphen gesehen und verstanden habt. In Video 6 lösen wir schließlich eine anspruchsvolle Textaufgabe.
Lineare Gleichungssysteme - Die drei Lösungsverfahren
Die 3 Lösungsverfahren in Kürze erklärt: Einsetzungsverfahren, Gleichsetzungsverfahren und Additionsverfahren
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
F06-2 Lineare Gleichungssysteme - Einsetzung und GleichsetzungEinsetzungsverfahren und Gleichsetzungsverfahren im Detail, Schnittpunkt von Graphen, Lineare Gleichungssysteme (LGS) mittels Funktionen dargestellt
-
F06-3 Lineare Gleichungssysteme - Additionsverfahren und FunktionenAdditionsverfahren mithilfe von Summenfunktion und Differenzfunktion erklärt
-
F06-4 Lineare Gleichungssysteme - Lösen mit AdditionsverfahrenAdditionsverfahren im Detail, Lösen mit dem Additionsverfahren inklusive vorheriger Umformung der linearen Gleichungen
-
F06-5 Lineare Gleichungssysteme - SubtraktionsverfahrenAdditionsverfahren als Subtraktionsverfahren (Betrachtung als Differenzfunktion), mögliche Lösungen für lineare Gleichungssysteme (Lösungsmenge/Lösungspaar)
-
F06-6 Lineare Gleichungssysteme - SachaufgabeAnwendung des linearen Gleichungssystems bei einer Sachaufgabe (Stausee), Lösung mit dem Subtraktionsverfahren
Zu den Linearen Gleichungssystemen haben wir hilfreiche Rechner für euch entwickelt, mit dem ihr eure Lösungen schnell überprüfen könnt.
Hier findest du 5 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 3 Lernchecks, mit denen du dein Wissen testen kannst.