Prozent - Einführung

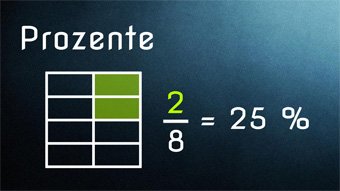
Zunächst ist verständlich zu machen, was Prozent überhaupt ist. Das Wort „Prozent“ stammt vom Lateinischen „pro centum“ und heißt übersetzt:

„pro“ = für/von   |   „centum“ = hundert

Das Wort „Prozent“ können wir uns entsprechend als „je Hundert“ merken.

Die Prozentrechnung befasst sich also mit Anteilen an Gesamtmengen, wobei diese auf 100 angepasst werden.

Haben wir zum Beispiel 20 Autos (Anteil) von 50 Autos (Gesamtmenge), so können wir dies in Prozent so ausdrücken:

Anteil : Gesamtmenge
20 Autos : 50 Autos → Gesamtmenge anpassen auf 100 Autos, also:

= 20 : 50      | anpassen auf :100
= 20·2 : 50·2
= 40 : 100
= 40 %

20 Autos von 50 Autos sind also 40 %.

Vorab: Es ist hilfreich, vorab bereits Folgendes zu wissen:

• Die Gesamtmenge ist 100 %.
• Die Hälfte der Gesamtmenge ist 50 %.
• Besitzt man keinen Anteil an der Gesamtmenge, so hat man 0 %.

Prozentzeichen

Das Prozentzeichen % geht aus der Abkürzung „cto“ hervor, was „per cento“ heißt (italienisch). Diese drei Buchstaben wurden leicht umgeformt und bilden heute das Prozentzeichen.

Wir schreiben anstelle von 100 Prozent (100 cto) wesentlich kürzer: 100 %

1 Prozent als 1 von 100

Betrachten wir:

1 %

Dies bedeutet 1 von 100 bzw. 1 Teil von 100 Teilen, also:

1 von 100

Aus der Bruchrechnung ist bekannt, dass man 1 von 100 auch als Division (Verhältnis) schreiben kann:

\( \frac{1}{100} \)

Wir müssen uns an dieser Stelle unbedingt merken:

1 % = 1 : 100 = \( \frac{1}{\textcolor{blue}{100}} \)

Hier erkennen wir, dass sich das Prozentzeichen als :100 schreiben lässt.

Auf diese Art kann man jede beliebige Prozentzahl in einen Bruch umwandeln. Zum Beispiel:

5 % = 5 : 100 = 5 · \( \frac{1}{\textcolor{blue}{100}} \) = \( \frac{5}{\textcolor{blue}{100}} \)

Und im Allgemeinen erhalten wir so:

x % = x : 100 = x · \( \frac{1}{\textcolor{blue}{100}} = \frac{x}{\textcolor{blue}{100}} \)