Lektion G32: Binärzahlen und Dezimalzahlen
Damit ihr mit Binärzahlen umgehen könnt, müsst ihr euch mit den Potenzen ein wenig auskennen, denn diese benutzen wir, um eine Binärzahl „lesbar“ zu machen, also in eine uns verständliche Zahl (eine Dezimalzahl) umzuwandeln. Alle notwendigen Details findet ihr in den Videos.
Im ersten Video schauen wir uns die Umrechnung der Binärzahl 1001 zur Dezimalzahl 9 an: 10012 = 1·23 + 0·22 + 0·21 + 1·20 = 910 und es gibt einen Tipp, wie ihr Binärzahlen ohne langes Rechnen sehr schnell umwandeln könnt.
Einführung der Binärzahlen mit Hilfe der Dezimalzahlen
Was ist eine Binärzahl, was ist eine Dezimalzahl. Begriffe Binärsystem, Dualsystem, Zweiersystem. Zerlegen einer Dezimalzahl in Zehnerpotenzen, Stellenwertsystem erklärt, Zweierpotenzen beim Binärsystem. Beispiel einer Umrechnung von Binär- zu Dezimalzahl.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G32-2 Dezimalzahlen in Binärzahlen umwandelnUmwandeln der Dezimalzahl 178 in die Binärzahl 10110010. Zerlegung der Dezimalzahl in eine Summe von Zweierpotenzen, Rechenweg erklärt. Alternative Rechenmethode über das Divisionsverfahren (Restverfahren).
-
G32-3 Binärzahlen addieren und subtrahierenAddition von Binärzahlen wie bei den Dezimalzahlen, einzelnen Stellen addieren mit Übertrag. Andere Rechenmethode bei Subtraktion: Wir splitten den Minuenden solange auf, bis der Subtrahend ziffernweise von ihm abgezogen werden kann. Nach dem Abzug addieren wir alle Stellen zusammen.
-
G32-4 Binärzahlen multiplizieren und dividierenSchriftliche Multiplizieren von Binärzahlen wie bei Dezimalzahlen, wir multiplizieren die einzelnen Stellen mit dem ersten Faktor. Anschließend addieren wir alle Ziffern stellenweise zusammen. Die Division wird gleichfalls schrittweise wie bei den Dezimalzahlen ausgeführt.
-
G32-5 Von der Binärzahl zur Dezimalzahl mittels Horner-SchemaDas Horner-Schema zerlegt Potenzen sinnvoll in Multiplikationen. Wiederholte Anwendung des Schemas in der Reihenfolge: mal 2, plus nächste Ziffer, Klammern herum. So erhalten wir den Dezimalwert der Binärzahl.
-
G32-6 Oktalzahlen und HexadezimalzahlenUmwandeln von Dezimalzahlen in Oktalzahlen und in Hexadezimalzahlen. Erklärung der einzelnen Schritte über die Summen von Potenzen. Zusätzlich die Umrechnung von Oktal- und Hexadezimalzahlen in Dezimalzahlen.
Mit dem Zahlenkonverter kann man Binärzahlen, Dezimalzahlen, Hexadezimalzahlen und Oktalzahlen ineinander überführen. Dort auf der rechten Seite findet ihr zusätzlich einen kleinen "Zahlenrechner". Hinter ihm verbirgen sich: Binärrechner, Dezimalrechner, Hexadezimalrechner und Oktalrechner für zwei ganze positive Zahlen.
-
 ZahlenkonverterHier könnt ihr beliebige Zahlen online in andere Zahlensysteme umwandeln. Der Zahlenkonverter übernimmt Binärzahlen, Dezimalzahlen, Hexadezimalzahlen und Oktalzahlen.
ZahlenkonverterHier könnt ihr beliebige Zahlen online in andere Zahlensysteme umwandeln. Der Zahlenkonverter übernimmt Binärzahlen, Dezimalzahlen, Hexadezimalzahlen und Oktalzahlen. -
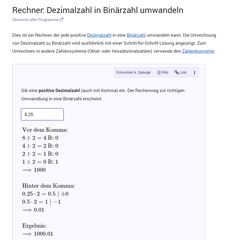 Rechner: Dezimalzahl in Binärzahl umwandelnDer Rechner kann jede positive Dezimalzahl in eine Binärzahl umwandeln.
Rechner: Dezimalzahl in Binärzahl umwandelnDer Rechner kann jede positive Dezimalzahl in eine Binärzahl umwandeln. -
 Rechner: Dezimalwert von BinärzahlenDies ist ein kleiner Rechner, der den Dezimalwert einer Binärzahl ermittelt.
Rechner: Dezimalwert von BinärzahlenDies ist ein kleiner Rechner, der den Dezimalwert einer Binärzahl ermittelt. -
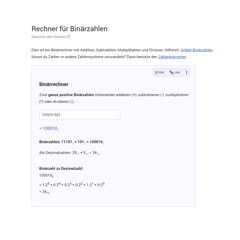 Rechner für BinärzahlenDies ist ein Binärrechner mit Addition, Subtraktion, Multiplikation und Division.
Rechner für BinärzahlenDies ist ein Binärrechner mit Addition, Subtraktion, Multiplikation und Division.
Hier findest du 4 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 4 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.





