Wir haben uns angeschaut, wir wir Binärzahlen in Dezimalzahlen umwandeln können. Den entsprechenden Artikel sollte man kennen, damit man die folgenden Inhalte verstehen kann.
Wir betrachten uns als nächstes, wie wir aus einer Dezimalzahl eine Binärzahl bilden.
Hierfür sei zuerst der Begriff „Zweierpotenz“ eingeführt:
Eine Zweierpotenz meint die mehrfache Multiplikation der 2 mit sich selbst.
Zweierpotenzen sind demnach: 2, 4, 8, 16, 32, 64, …
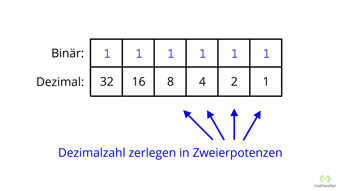
Wie wir gesehen haben, steht jede Stelle einer Binärzahl für eine Zweierpotenz:

Dabei haben wir die Stellen addiert, um auf den Dezimalwert zu kommen.
Zum Beispiel für die Binärzahl 101010:
1·32 + 0·16 + 1·8 + 0·4 + 1·2 + 0·1 = 32 + 8 + 2 = 42
Und genau diesen Rechenweg müssen wir jetzt „rückwärts“ gehen, um aus einer Dezimalzahl eine Binärzahl zu bilden.
Wir zerlegen die Dezimalzahl in eine Summe von Zweierpotenzen. Dabei fangen wir mit der größtmöglichen Zweierpotenz an.
Vorgehen
Zur Umwandlung einer Dezimalzahl in eine Binärzahl gehen wir also wie folgt vor (als Beispiel nehmen wir die Dezimalzahl „78“):
-
Wir schauen, welche die größtmögliche Zweierpotenz ist, die in die 78 hineinpasst:
1, 2, 4, 8, 16, 32, 64, 128, …
Offensichtlich ist dies die 64.
-
Als nächstes ziehen wir die gefundene Zweierpotenz von unserer Dezimalzahl ab, also:
78 - 64 = 14
Bzw. wir schreiben 78 nun so:
78 = 64 + 14
-
Den Rest 14 müssen wir nun ebenfalls weiter in Zweierpotenzen zerlegen. Schauen wir, welche die größtmögliche Zweierpotenz ist:
1, 2, 4, 8, 16, 32, 64, 128, …
Offensichtlich ist dies die 8.
-
Als nächstes schreiben wir die 78 mit den gefundenen Zweierpotenzen, also:
78 = 64 + 8 + 6
-
Den Rest 6 zerlegen wir nun weiter in Zweierpotenzen. Schauen wir, welche die größtmögliche Zweierpotenz ist:
1, 2, 4, 8, …
Offensichtlich ist dies die 4.
-
Als nächstes schreiben wir die 78 mit den gefundenen Zweierpotenzen, also:
78 = 64 + 8 + 4 + 2
Der Rest 2 ist eine Zweierpotenz und muss nicht weiter zerlegt werden.
-
Jetzt haben wir also die Dezimalzahl 78 in Zweierpotenzen zerlegt und können die Binärzahl bilden. Hierzu nehmen wir uns eine Tabelle zur Hand:
Zweierpotenzen: 64 32 16 8 4 2 1 Binärzahlen: -
Nun tragen wir dort eine 1 ein, wo unsere ermittelten Zweierpotenzen 64 + 8 + 4 + 2 (= 78) übereinstimmen. Ansonsten eine 0:
Zweierpotenzen: 64 32 16 8 4 2 1 Binärzahlen: 1 0 0 1 1 1 0 -
Im letzten Schritt notieren wir die ermittelte Binärzahl (aus der vorigen Tabelle):
1001110