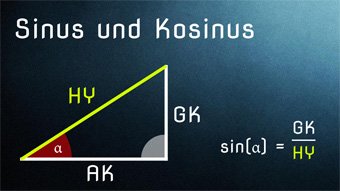
Vorab sei erwähnt, dass wir im Folgenden nur rechtwinklige Dreiecke betrachten. Ein Winkel im Dreieck muss also 90° groß sein, meist wird er als Gamma γ bezeichnet, damit sind die beiden anderen Winkel Alpha α und Beta β kleiner als 90°. Erinnern wir uns hier an den Winkelsummensatz: α + β + γ = 180°. Wenn γ = 90°, dann α + β + 90° = 180° und α + β = 90°.
Vielen Schülern fällt der Einstieg in die Trigonometrie schwer, da sie schon bei den Bezeichnungen am Dreieck Schwierigkeiten haben. Erklären wir also einfach:
Die längste Seite in einem rechtwinkligen Dreieck wird immer „Hypotenuse“ genannt (der Begriff bedeutet „die Ausgestreckte“). Die anderen beiden Seiten werden allgemein „Katheten“ genannt.
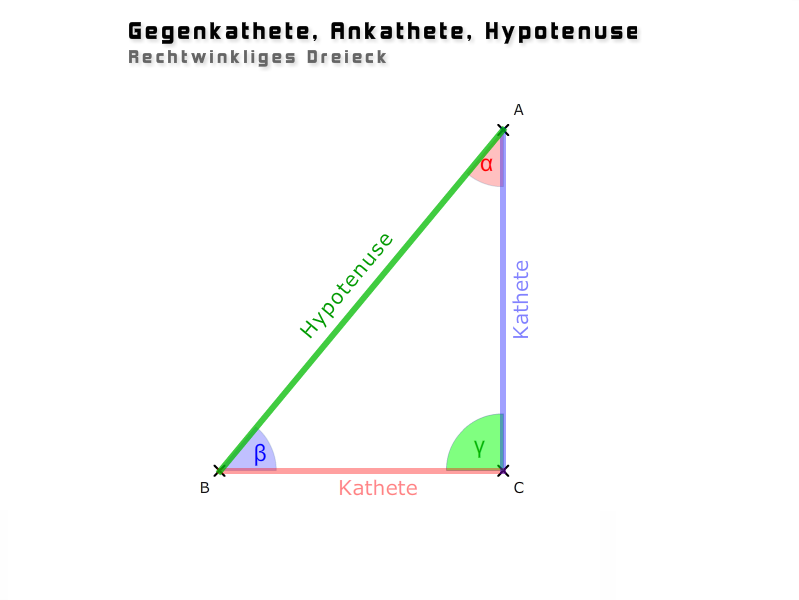
Jetzt kommt es darauf an, welchen Winkel α oder β wir uns betrachten. Je nach gewähltem Winkel kann jede Kathete entweder Ankathete oder Gegenkathete heißen.
Wählen wir uns Beta β aus, dann ergibt sich:
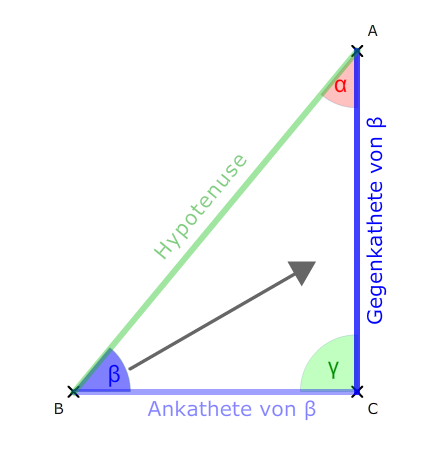
Wir erkennen, dass die Seite, die dem Winkel β direkt gegenüber liegt, die Gegenkathete ist. Und dass die Seite, die dem Winkel β anliegt die Ankathete ist.
Wählen wir uns Alpha α aus, dann ergibt sich:
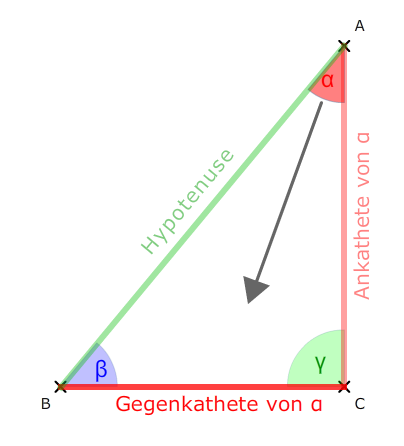
Wir erkennen, dass die Seite, die dem Winkel α direkt gegenüber liegt, die Gegenkathete ist. Und dass die Seite, die dem Winkel α anliegt die Ankathete ist.
Bedenken wir, dass man die Dreiecke auch drehen kann und die Bezeichnungen dabei gleich bleiben:
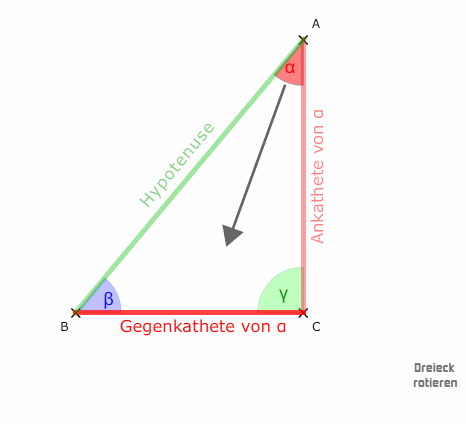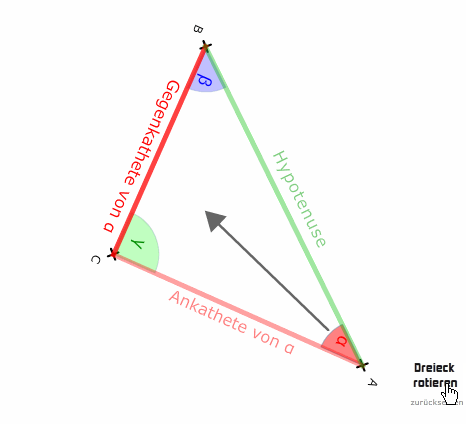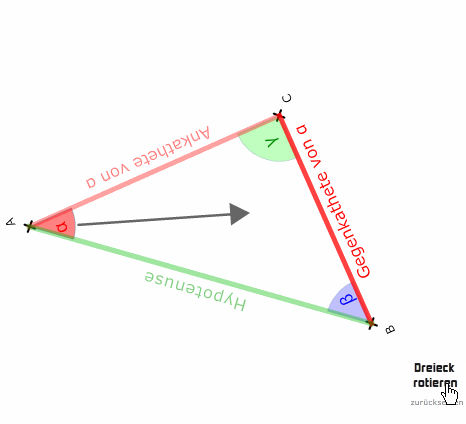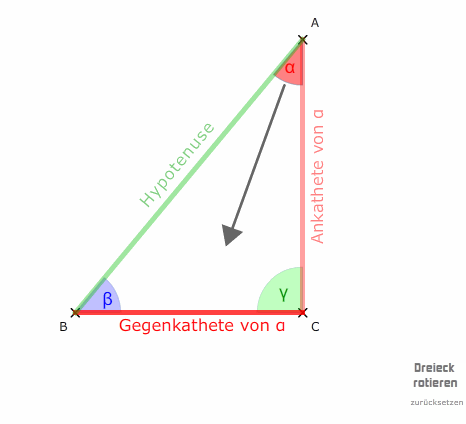
An einem Winkel im Dreieck liegen stets Ankathete und Hypotenuse an. Die Gegenkathete berührt den Winkel nie!
Der längsten Seite (Hypotenuse) liegt immer der rechte Winkel gegenüber. Bzw. dem rechten Winkel liegt immer die längste Seite gegenüber.