Manchmal stößt man auf solche Angaben von Sinuswerten:
sin(45°) = 1/2 · √2 ≈ 0,707
Um zu verstehen, warum hier eine Wurzel verwendet wird, erinnern wir uns an die Sehnenfunktion (Chord). Dort hatten wir einen Kreis kennen gelernt, bei dem wir zwei Punkte gegenüber gesetzt haben und auf diese Weise zwei rechtwinklige Dreiecke erzeugen konnten.
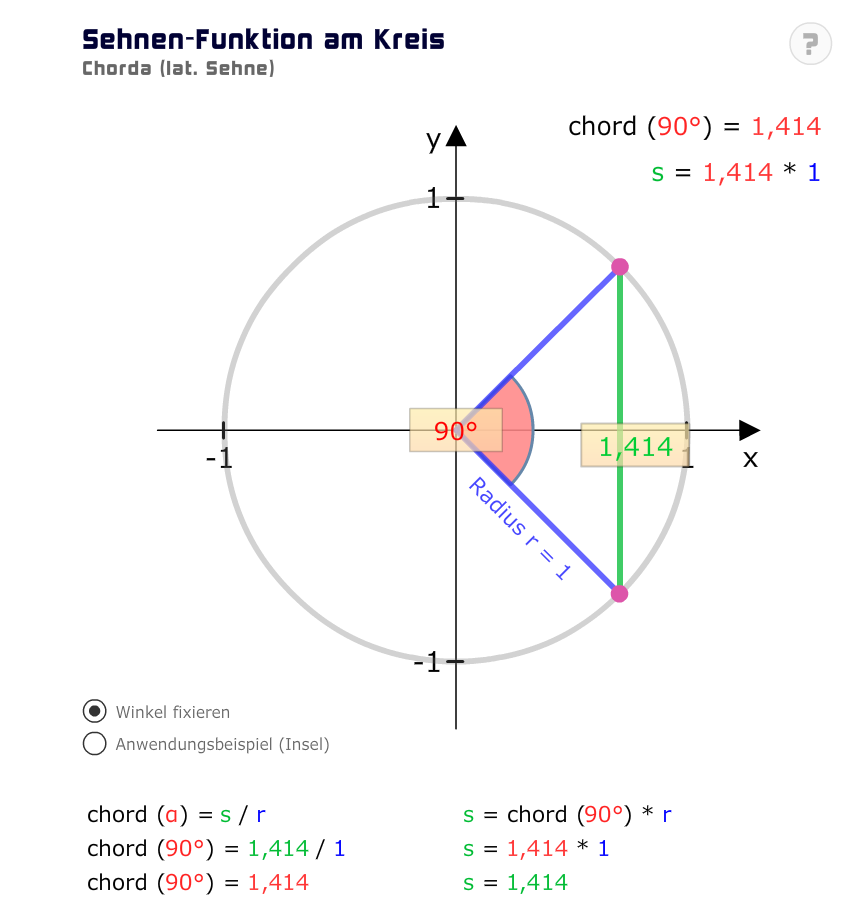
Wenn wir einen Winkel von 90° haben, dann ist die Hälfte 45° und es ergibt sich die grüne Strecke mit ca. 1,414. Ursache dessen ist, dass wir aufgrund des rechten Winkels den Satz des Pythagoras anwenden können (Radius): 1² + 1² = c²
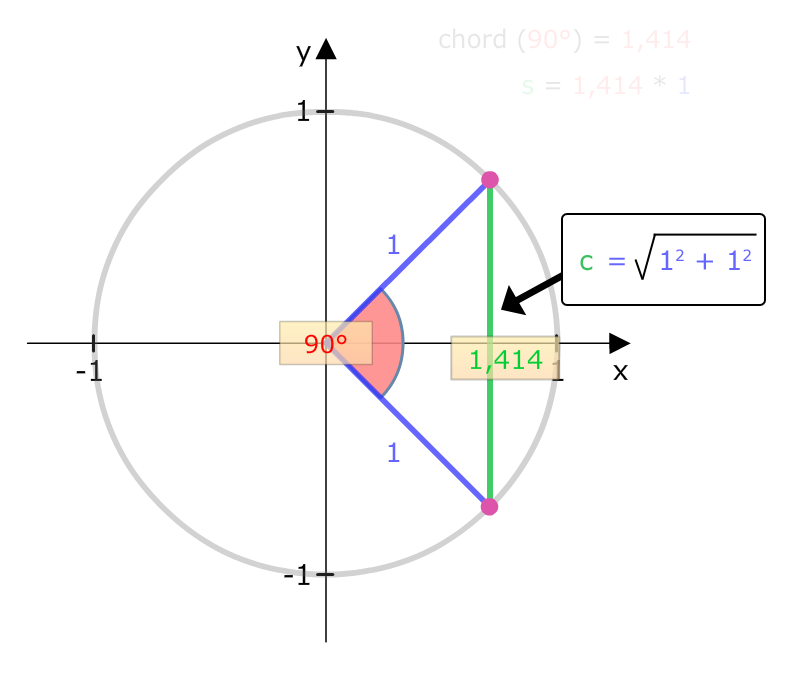
Die Strecke c ergibt sich also aus √(1² + 1²). Und das ist die Wurzel aus 2, also rund 1,414.
Die Hälfte dieser Strecke ist 1/2 · √2. Deshalb ist sin(45°) = 1/2·√2 ≈ 0,707.