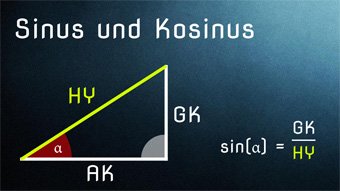
Jetzt können wir statt dem Verhältnis Gegenkathete / Hypotenuse das Verhältnis aufstellen: Ankathete / Hypotenuse.
Werfen wir noch einmal einen Blick auf die Werte bei den verschiedengroßen Dreiecken, die alle den Winkel Beta β = 30° gemeinsam haben:
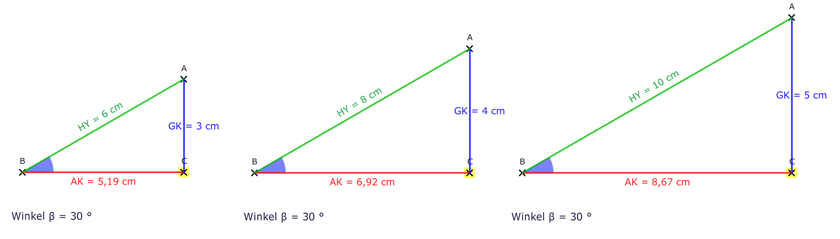
Es zeigen sich folgende Verhältniswerte:
AK/HY = 5,19 cm/6 cm = 6,92 cm/8 cm = 8,67 cm/10 cm ≈ 0,867.
Also immer 0,867 und zwar egal, welche Dreiecksgröße wir wählen.
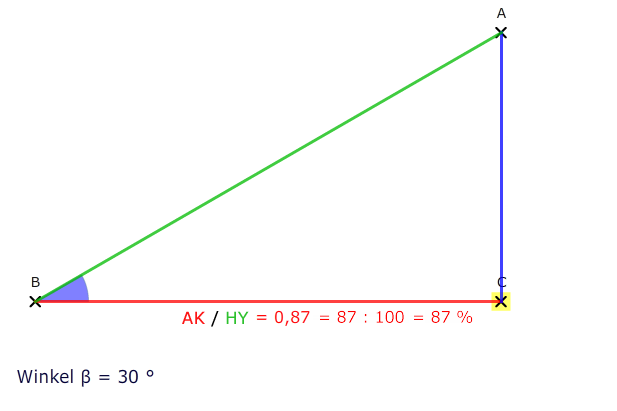
Dieses Verhältnis nennen wir den Kosinuswert und schreiben: cos(30°) ≈ 0,867
Die Formel für den Kosinus lautet allgemein:
cos(α) = Ankathete/Hypotenuse
Auch hier gibt uns der Wert an, wie lang die Ankathete im Vergleich zur Hypotenuse ist.
Haben wir einen Winkel von 30° und wir wissen, die Hypotenuse ist 10 cm lang, so können wir aufstellen: cos(30°) = 0,867 = AK/HY. Damit ist die Ankathete AK = 0,867·HY.
Die Ankathete ist also 0,867 mal so lang wie die Hypotenuse (0,867 = 86,7 % von ihrer Länge).
Mit den Werten: AK = 0,867·HY = 0,867·10 cm = 8,67 cm (als Länge der Ankathete).