„Runden“ meint das Erhöhen oder Verringern einer Zahl auf einen Wert („Näherungswert“), sodass alle Stellen kleiner als die zu rundende Stelle 0 sind.
Beispiel für Abrunden: 96 127 ist rund 96 000.
Beispiel für Aufrunden: 14 973 ist rund 15 000.
Das Runden von natürlichen Zahlen hilft uns, unhandliche Zahlen zu vereinfachen und übersichtlicher zu machen. Wir können gerundete Zahlen leichter lesen und uns einfacher merken, auch das Vergleichen fällt einfacher.
Beispiele aus dem Alltag:
- „Unsere Schule hat rund 300 Schüler.“ (Statt der exakten 312 Schüler.)
- „Berlin hat rund 3 600 000 Einwohner.“ (Statt 3 575 000 Einwohner.)
- „Wir fahren rund 70 km/h.“ (Statt der genauen 73 km/h.)
Vorwissen
Erinnern wir uns an das Stellenwertsystem, dort haben wir gelernt, dass jede Ziffer innerhalb einer Zahl einen Wert hat.
Zum Beispiel steht die Ziffer 5 bei der Zahl 15 333 auf der Tausenderstelle. Ihr Wert ist also 5·1000 = 5 000.
Der Wert einer Ziffer ergibt sich also stets danach, auf welcher Stelle sie steht (Zehnerstelle, Hunderterstelle, Tausenderstelle usw.).

Was ist Runden
Beim Runden ändern wir den Wert einer Zahl so, dass er „rund“ wird. Dabei wird der Wert einer Zahl nach folgenden Regeln verändert:
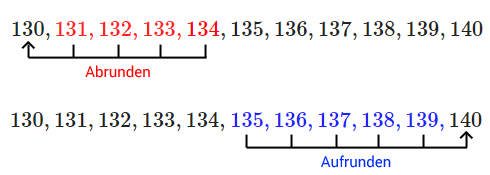
Abrunden: Beispiel: 132 ist rund 130.
Wenn auf der Stelle eine 1, 2, 3, 4 steht, dann vermindern wir die Zahl.
Aufrunden:
Beispiel: 139 ist rund 140.
Wenn auf der Stelle eine 5, 6, 7, 8, 9 steht, dann erhöhen wir die Zahl.
Das heißt, die Rundungsstelle (hier die Zehnerstelle) wird um +1 erhöht.
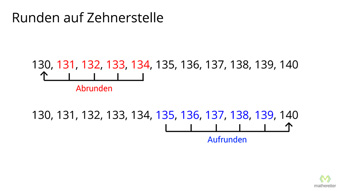
Als Auflistung für jede einzelne Zahl:
- 130 ist 130
- 131 ist rund 130
- 132 ist rund 130
- 133 ist rund 130
- 134 ist rund 130
- 135 ist rund 140
- 136 ist rund 140
- 137 ist rund 140
- 138 ist rund 140
- 139 ist rund 140
- 140 ist 140
Wir können eine Zahl auf eine beliebige Stelle „runden“: Zehnerstelle, Hunderterstelle, Tausenderstelle usw. In den obigen Beispielen haben wir auf die Zehnerstelle (10, 20, 30, …) gerundet. Wie wir auf Hunderterstelle runden, erfahren wir im Folgenden.
Rundungsbeispiele
Runden auf Zehner
Die Zahl 134 soll auf die Zehnerstelle (die 3) gerundet werden.
Müssen wir zur 130 abrunden oder zur 140 aufrunden?
Als erstes schauen wir uns die Stelle rechts von der 3 an (es ist die Einerstelle mit 4).
Wir erkennen, dass bei 4 abgerundet werden muss, das heißt die 4 wird zu 0.
130 ← (abrunden) 134
Ergebnis: 134 ist rund 130.
Schreibweise für das Runden: 134 ≈ 130
Das Zeichen ≈ heißt „Rundungszeichen“. Man sagt dazu „ungefähr gleich“.
Wie gesagt, müssen wir bei Ziffern von 4 und kleiner abrunden und ab der Ziffer 5 aufrunden:

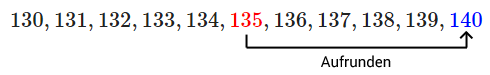
Runden auf Hunderter
Die Zahl 2 791 soll auf die Hunderterstelle (die 7) gerundet werden.
Müssen wir zur 2 700 abrunden oder zur 2 800 aufrunden?
Als erstes schauen wir uns die nächstkleinere Stelle (die Zehnerstelle mit 9) an.
Wir erkennen, dass wir bei 9 aufrunden müssen, das heißt die 91 wird zur 100 bzw. die 791 wird zur 800. Es gilt für die gesamte Zahl demnach:
2791 (aufrunden) → 2800
Ergebnis: 2 791 ist rund 2 800.
Schreibweise für das Runden: 2 791 ≈ 2 800
Beim Runden müssen wir immer direkt auf die Ziffer hinter der Rundungsstelle schauen, alle anderen Stellen weiter rechts können wir vernachlässigen.
Runden einer Zahl auf mehrere Stellen
Exakte Zahl: 72 891
Rundung auf 10er: 72 890
Rundung auf 100er: 72 900
Rundung auf 1 000er: 73 000
Rundung auf 10 000er: 70 000
Rundung auf 100 000er: 100 000
Rundungsrechner
Gib eine Zahl ein, das Programm rundet sie auf die entsprechenden Stellen: