Wir haben gelernt, dass sich die natürlichen Zahlen mit den Ziffern 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 darstellen lassen. Mit diesen Ziffern können wir beliebige Zahlen bilden. Ein paar Beispiele sind: 10, 25, 67, 120, 1 248, …
Wir können die Zahlen der Größe nach an einem „Zahlenstrahl“ abtragen. Ein Zahlenstrahl ist ein Strahl, auf dem jeder gesetzte Strich für eine Zahl steht.
Der Zahlenstrahl beginnt bei der Zahl 0 und geht in gleichen Abständen nach rechts weiter mit 1, 2, 3, 4, …
Der Abstand von Strich zu Strich kann zum Beispiel 1 cm sein. Wir nennen diesen einheitlichen (also immer gleichen) Abstand die „Einheitsstrecke“.
Je weiter rechts wir auf dem Zahlenstrahl sind, desto größer ist die dortige Zahl. Den Zahlenstrahl können wir übrigens nach rechts beliebig verlängern, da es unendlich viele natürliche Zahlen gibt.
Wir können statt 0 auch einen anderen Startwert wählen und außerdem einen anderen Zählabstand von einem Strich zum anderen Strich (z. B. 5). Zeichnen wir bspw. einen Zahlenstrahl, der bei 300 beginnt und 5er-Schritte als Abstand hat.
Der Zahlenstrahl ist eine praktische Hilfe, denn wir können darauf beliebige Zahlen eintragen. Zudem hilft er uns zu erkennen, welche Zahl größer ist, denn das ist immer die Zahl, die weiter rechts liegt.
Zahl am Zahlenstrahl abtragen
Um eine natürliche Zahl an der richtigen Position auf dem Zahlenstrahl einzutragen, müssen wir zuerst schauen, welche Zahl uns gegeben ist. Nehmen wir als Beispiel die 36. Dann betrachten wir den Zahlenstrahl, wie dieser aufgebaut ist. Das heißt, welche Zahlen sind schon eingetragen. Ein Beispiel eines solchen Zahlenstrahls:
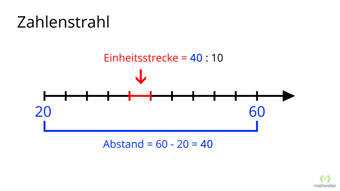
Wir sehen, dass dieser Zahlenstrahl bei 20 beginnt und bei 60 aufhört. Außerdem können wir abzählen, dass 10 Abstände abgetragen worden sind:
Das heißt, mit 10 Abständen (Schritten) laufen wir von 20 bis 60, also 60 - 20 = 40 Zahlen weiter.
Den Abstand von einem Strich zum nächsten Strich ist also 40 Zahlen : 10 Abstände = 4 Zahlen je Abstand. Das heißt, der gleiche Abstand (die Einheitsstrecke) ist 4 lang. Nun können wir diese 4er-Schritte abtragen:
Jetzt sehen wir auch gut die Position der Zahl 36, die wir eintragen können.