Lektion G09: Rechnen mit Kommazahlen
Es lässt sich leider immer wieder feststellen, dass Schüler oft nur noch den Taschenrechner benutzen und nicht mehr wissen, wie man Kommazahlen mit Papier, Stift und Köpfchen eigentlich rechnet. Die folgenden Videos holen in Erinnerung, wie das Rechnen mit Komma funktioniert. Mit Kommas rechnen zu können, ist wesentliche Grundlage der Mathematik.
Weitere Videos für Kunden:
-
G09-1 Rechnen mit Kommazahlen - Einführung und RegelnEinführung zum Rechnen mit Kommazahlen, Bestandteile der Kommazahl, Regeln für die Addition, Subtraktion, Multiplikation und Division von Kommazahlen.
-
G09-2 Rechnen mit Kommazahlen - Rechenregeln + DezimalbrücheAdditionsregel und Multiplikationsregel erläutert, Dezimalbrüche (Dezimalzahlen), Umwandlung zwischen Kommazahl ↔ Bruch, Kommazahlen als Brüche rechnen.
-
 Rechnen mit KommazahlenHier könnt ihr zwei Kommazahlen miteinander addieren oder subtrahieren, inklusive Übertrag und Ergebnis.
Rechnen mit KommazahlenHier könnt ihr zwei Kommazahlen miteinander addieren oder subtrahieren, inklusive Übertrag und Ergebnis. -
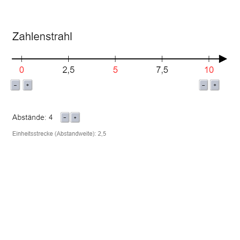 Kommazahlen am ZahlenstrahlHier werden Kommazahlen am Zahlenstrahl dargestellt. Abstände können verändert werden.
Kommazahlen am ZahlenstrahlHier werden Kommazahlen am Zahlenstrahl dargestellt. Abstände können verändert werden. -
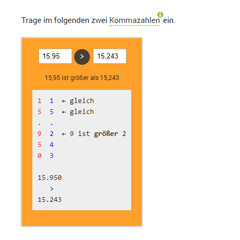 Kommazahlen vergleichenHier könnt ihr zwei Kommazahlen in ihrer Größe miteinander vergleichen.
Kommazahlen vergleichenHier könnt ihr zwei Kommazahlen in ihrer Größe miteinander vergleichen. -
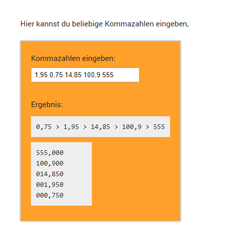 Kommazahlen sortierenDer Rechner kann beliebig viele Kommazahlen der Größe nach sortieren.
Kommazahlen sortierenDer Rechner kann beliebig viele Kommazahlen der Größe nach sortieren.
Hier findest du 11 Arbeitsblätter, mit denen du dein Wissen testen kannst.
-
AB: Lektion Kommazahlen (Teil 1)
-
AB: Lektion Kommazahlen (Teil 2)
-
AB: Lektion Kommazahlen (Teil 3)
-
AB: Lektion Kommazahlen (Teil 4)
-
AB: Kommazahlen am Zahlenstrahl ablesen
-
AB: Kommazahlen vergleichen und ordnen
-
AB: Kommazahlen runden
-
AB: Kommazahlen sinnvoll runden
-
AB: Vorteile und Nachteile beim Runden von Zahlen
-
AB: Kommazahlen im Alltag
-
AB: Besonderheit von Kommazahlen
Hier findest du 8 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Kommazahlen - Einführung
- Kommaverschiebung
- Addition von Kommazahlen
- Subtraktion von Kommazahlen
- Multiplikation von Kommazahlen
- Division von Kommazahlen
- Schriftliche Multiplikation von Kommazahlen
- Schriftliche Division von Kommazahlen
- Multiplikation von Null-Komma-Zahlen
- Kommazahlen am Zahlenstrahl
- Kommazahlen am Zahlenstrahl ablesen
- Kommazahlen am Zahlenstrahl eintragen
- Kommazahlen vergleichen
- Kommazahlen ordnen
- Kommazahlen runden
- Kommazahlen sinnvoll runden
- Vorteile und Nachteile beim Runden von Zahlen
- Kommazahlen im Alltag
- Besonderheit von Kommazahlen
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.


