Die Wurzel macht das Potenzieren rückgängig.
Ziehen wir die Wurzel aus dem Potenzwert, so erhalten wir die ursprüngliche Basis.
Das Zeichen für die Operation „Wurzelziehen“ ist: \( \sqrt{ \phantom{x} } \)
Was das bedeutet, zeigt uns folgendes Beispiel:
$$ \textcolor{#00F}{3}^{ \textcolor{#F00}{2} } = \textcolor{#080}{9} \xrightarrow{rückgängig} \sqrt [ \textcolor{#F00}{2} ]{ \textcolor{#080}{9} } = \textcolor{#00F}{3} $$
Nun andersherum gelesen:
$$ \sqrt [ \textcolor{#F00}{2} ]{ \textcolor{#080}{9} } = \textcolor{#00F}{3} \xrightarrow{denn} \textcolor{#00F}{3}^\textcolor{#F00}{2} = \textcolor{#080}{9} $$
Ein weiteres Beispiel:
$$ \sqrt [ \textcolor{red}{3} ]{ \textcolor{#080}{64} } = \textcolor{#00F}{4} \xrightarrow{denn} \textcolor{#00F}{4}^\textcolor{red}{3} = \textcolor{#080}{64} $$
Es gibt drei wichtige Begriffe für die Wurzel, die wir kennen müssen:
- Basis
- Wurzelexponent
- Wurzelwert
Diese Begriffe sind in der Abbildung zugeordnet:
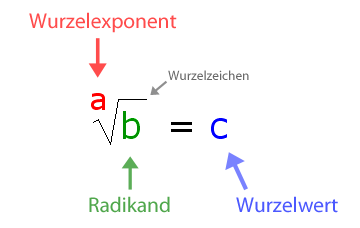
Der „Radikand“ ist die Zahl unterhalb des Wurzelzeichens, also die Zahl, aus der wir die Wurzel ziehen sollen.
Allgemeiner Zusammenhang zwischen Wurzel und Potenz:
$$ \sqrt [ \textcolor{#F00}{a} ]{ \textcolor{#080}{b} } = \textcolor{#00F}{c} \rightarrow \textcolor{#00F}{c}^\textcolor{#F00}{a} = \textcolor{#080}{b} $$
wobei der Radikand b immer positiv sein muss.

