Beim Umformen von Gleichungen mit Hilfe des Wurzelziehens müssen wir ein positives und negatives Ergebnis mit ± (Plus-Minus) berücksichtigen. Zum Beispiel bei der Gleichung:
x² = 4
Fragen wir danach, welche Zahlen ins Quadrat 4 ergeben? Richtig, das sind 2 und -2. Denn:
(+2)² = 4
(-2)² = 4
Nachfolgend in der Abbildung dargestellt:
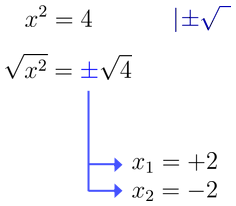
Man spricht hier von der Mehrdeutigkeit der Wurzel (Fachbegriff Ambiguität). Merken wir uns:
Eine reelle Zahl (positiv oder negativ) ergibt quadriert immer den gleichen positiven Wert. Wenn wir jedoch eine Wurzel aus einer Zahl ziehen, dann gibt es zwei mögliche Lösungen (eine positive und eine negative).
Korrekte Schreibweise
Die Schreibweise beim Beispiel oben mit ±√ ist mathematisch nicht ganz korrekt. Für die korrekt Schreibweise nutzt man den Betrag. Denn mit Hilfe vom Betrag von x erhalten wir das positive und das negative Ergebnis:
$$ \quad x^2 = 4 \qquad |\,\sqrt{\phantom{0}} \\ \sqrt{x^2} = \sqrt{4} \qquad | \text{ Betrag} \\ \quad |x| = \sqrt{4} \\[15pt] \implies { x _ { 1 } = + 2 } \text{ und } { x _ { 2 } = - 2 } $$
