Lektion F02: Lineare Funktionen - Einführung
Nachdem wir jetzt verstanden haben, wie das kartesische Koordinatensystem funktioniert, legen wir richtig los: Es folgt die Einführung zu den linearen Funktionen.
Lineare Funktionen - Einführung
Was ist f(x), gesprochen "f von x". Wie entsteht eine Funktionsgleichung und wie ergibt sich die Steigung eines Graphen. Was ist ein Steigungsdreieck. Steigung einer linearen Funktion ermitteln.
Zugriff auf Video nur als eingeloggter Benutzer.
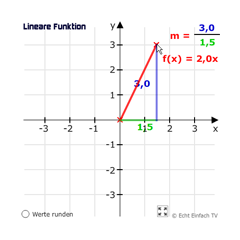
In dem folgenden Koordinatensystem könnt ihr selbst die Steigung betrachten. Bewegt die Maus und ihr seht die Abstände für x und y und die sich ergebende Steigung m - das ist der Wert, der vor dem x steht. Die Werte können auf ganze Zahlen gerundet werden. Dazu unten links im Programm „Werte runden“ aktivieren.
Da der Graph (die rote Linie) durch den Koordinatenursprung (0 | 0) geht, können wir die einfache Form von f(x) = m·x verwenden. Wann wir die Form f(x) = m·x + n benutzen, erfahrt ihr in der nächsten Lektion.
Hier findest du 4 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.