Teilbarkeit durch 7

Hier stellen wir drei Verfahren vor, um die Teilbarkeit durch 7 zu prüfen.

Der erste Merksatz ist nicht ganz so einfach, aber mit den Beispielen unten versteht man ihn besser.

Beispiele

Die Probe ist korrekt, wenn bei der Division eine ganze Zahl herauskommt. Die Zahl ist dann durch die genannte Zahl teilbar.

• 875 Prüfen mit 75 + 2·8 = 91
  → 91 ist durch 7 teilbar, also ist auch 875 durch 7 teilbar ✓
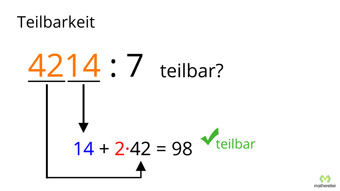
• 4 214 Prüfen mit 14 + 2·42 = 98
  → 98 ist durch 7 teilbar, also ist auch 4 214 durch 7 teilbar ✓
• 12 110 Prüfen mit 10 + 2·121 = 252
  → 252 ist durch 7 teilbar, also ist auch 12 110 durch 7 teilbar ✓
• 448 315 Prüfen mit 15 + 2·4483 = 8981
  → Verfahren nochmals durchführen:
  8 981 prüfen mit 81 + 2·89 = 259
  → 259 ist durch 7 teilbar, also ist auch 448 315 durch 7 teilbar ✓

Ist die Prüfzahl nicht einfach im Kopf durch 7 teilbar, so wiederholt man den Vorgang mit der Prüfzahl.
Für das Beispiel 12 110 → 252. Verfahren nochmals mit 252, also: 52 + 2·2 = 56, und 56 ist durch 7 teilbar.

Gegenbeispiele

Die Probe ist nicht korrekt, wenn bei der Division ein Rest übrig bleibt (bzw. sich eine Kommazahl ergibt). Die Zahl ist dann durch die genannte Zahl nicht teilbar.

• 2 117 Prüfen mit 17 + 2·21 = 59
  → 59 : 7 = 56 Rest 3 ✗
• 65 438 Prüfen mit 38 + 2·654 = 1 346
  → nochmals mit 1 346, also: 46 + 2·13 = 72 → 72 : 7 = 10 Rest 2 ✗
• 300 704 Prüfen mit 04 + 2·3007 = 6 018
  → nochmals mit 6 018, also: 18 + 2·60 = 138 → 138 : 7 = 19 Rest 5 ✗

Neben der oben vorgestellten Teilbarkeitsregel gibt es noch weitere, die meist komplizierter sind. Der Vollständigkeit halber stellen wir zwei weitere Verfahren vor:

Teilbarkeit durch 7 über das Doppelte der letzten Ziffer

Mithilfe dieses Verfahrens lässt sich ebenfalls die Teilbarkeit durch 7 prüfen. Wir nehmen das doppelte der letzten Ziffer und subtrahieren es von der aus allen vorderen Ziffern gebildeten Zahl, unter jeweiliger Wegnahme der letzten Ziffer (als Iteration).

Beispiel:

770 784 → 77 078 - 2·4 = 77 070
77 070 → 7 707 - 2·0 = 7 707
7 707 → 770 - 2·7 = 756
756 → 75 - 2·6 = 63

→ 63 ist :7 teilbar, also ist 770 784 auch :7 teilbar

Die Regel heißt: „Eine Zahl 10a + b ist genau dann durch 7 teilbar, wenn a − 2b durch 7 teilbar ist.“

Teilbarkeit durch 7 über Zerlegung in „Dreierblöcke“

Für dieses Verfahren zerlegen wir die zu prüfende Zahl in „Dreierblöcke“ und addieren diese „Dreierblöcke“ mit alternierenden (wechselndes) Vorzeichen:

7 770 784 → -7 + 770 - 784 = -21

Als nächstes prüfen wir, ob dieses Ergebnis durch 7 dividiert werden kann.

→ (-21) ist :7 teilbar ✓

→ also ist auch 7 770 784 durch :7 teilbar.