Lektion G17: Prozente / Prozentrechnung - Matheretter
Was ist Prozent und wie rechnet man damit? Was bedeutet Grundwert, Prozentwert und Prozentsatz. Häufige Fehler und Beispielaufgaben.
Matheretter
Lektion G17: Prozente / Prozentrechnung
Inhalte:
- Was ist Prozent und wo kommt das Prozentzeichen her?
- Wie rechnet man mit Prozenten?
- Was hat Prozent mit Zahlen und Brüchen zu tun?
- Wie wandelt man Prozent in eine Zahl um?
- Was sind Grundwert, Prozentwert und Prozentsatz?
- Wie leiten sich die Formeln für die Prozentrechnung her?
- Was sind häufige Fehlerquellen und wie vermeidet man sie?
Voraussetzung:
Laut Lehrplan: 6. - 7. Klasse
Die Prozentrechnung fällt einigen Schülern im Unterricht nicht leicht. Diese Lektion soll euch mit Videos und Lernprogrammen helfen, das Thema vollständig zu begreifen. So könnt ihr dann wesentlich bessere Mathenoten schreiben. Viel Spaß beim Verstehen.
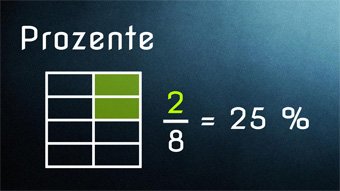
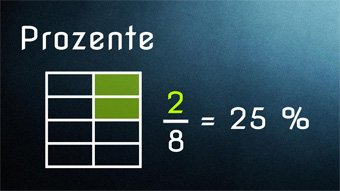
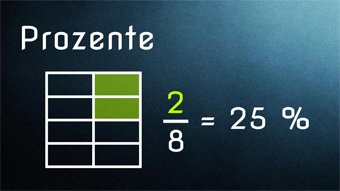
Prozentrechnung - Einführung Prozent %
Was ist Prozent, was bedeutet das Prozentzeichen, was sind Anteile, Zusammenhang zwischen Bruch, Prozent und Zahl.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G17-2 Prozentrechnung - Grundwert + ProzentwertÜber den Dreisatz zu den Formeln für Grundwert (Gesamtmenge) und Prozentwert (Anteil).
-
G17-3 Prozentrechnung - ProzentsatzHerleitung der Formel für den Prozentsatz, Aufgaben und Lösungen zur Prozentrechnung, Rechentricks für schnelleres Prozentrechnen.
-
G17-4 Prozentrechnung - Häufige FehlerquellenHäufige Fehlerquellen, Prozentsätze über 100 %, bequeme Prozentsätze, Lehrbücher mit Formeln ·100, Rechnen mit Promille.
-
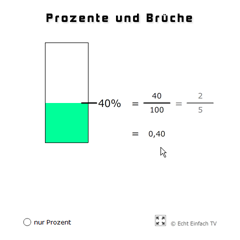Prozente und BrücheZusammenhang zwischen Prozent, Bruch und Zahl. -
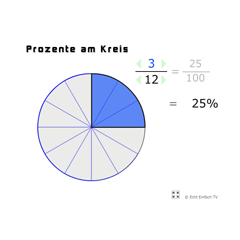Prozente und Brüche am KreisAm Kreis werden Bruch und Prozent verdeutlicht. -
Prozente anhand einer FlächeMarkiert einzelne Flächenteile und klickt auf 100%. Der sich ergebende Prozentsatz wird angezeigt. Die Stückelung der Fläche kann verändert werden. -
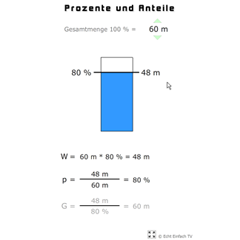Prozente und Anteile (Formeln)Wesentliche Formeln der Prozentrechnung für: Prozentwert, Prozentsatz und Grundwert. Beliebige Anteile können eingestellt werden, zeitgleich ändern sich die Werte der Formeln. -
Prozente: Prozentsatz (%) berechnenHier könnt ihr den Prozentsatz aus eigenen Werten für Prozentwert (Anteil) und Grundwert (Gesamtmenge) ermitteln. -
Prozente: Prozentwert (Anteil) berechnenMit diesem Programm kann der Prozentwert (Anteil) aus Prozentsatz und Grundwert errechnet werden. -
Prozente: Grundwert (Gesamtmenge) berechnenHier könnt ihr den Grundwert (Gesamtmenge) aus Prozentsatz und Prozentwert berechnen. -
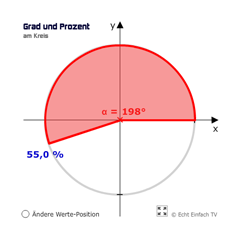Prozente und Grade am KreisDer Zusammenhang zwischen Grad und Prozentsatz am Kreis. Der gesamte Kreis sind die 100 % bzw. 360 Grad. -
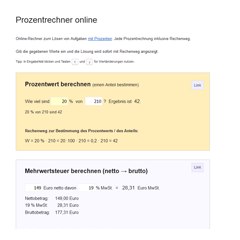ProzentrechnerProzente berechnen. Zum Beispiel: Wie viel sind 20 % Prozent von 210 Euro. Die Lösung wird euch komplett mit Rechenweg angezeigt.
Hier findest du 5 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Prozent - Einführung
- Umwandlung: Bruch zu Prozentzahl
- Umwandlung: Beliebige Zahl zu Prozentzahl
- Umwandlung: Kommazahl zu Prozentzahl
- Rechnen mit Prozenten (Prozentrechnung)
- Prozente: Grundwert gesucht
- Prozente: Prozentwert gesucht
- Prozente: Prozentsatz gesucht
- Prozentformeln in Übersicht
- Prozentaufgaben zur Übung
- Prozente über 100 %
- Bequeme Prozentsätze
- Häufige Fehlerquellen bei Prozenten
- Promille
Häufige Fragen:
- Wieviel Prozent sind 800 Tage von 3500 Tagen?
- Wie kann ich Prozente für Preisänderungen berechnen (Euro je Liter Benzin)?
- Wieviel Gramm Wasser enthalten beide Bananen zusammen?
- Wie kann ich herausfinden, was Prozentsatz ist und was Prozentwert ist?
- Wie kann ich Brüche in Prozentangaben umwandeln?
- Preis stieg um 10% auf 1375 Euro. Wie hoch war der Preis vorher?
- Welche Zahl minus 19 Prozent ergibt 500?
Finde weitere Fragen und Antworten in der Mathelounge.