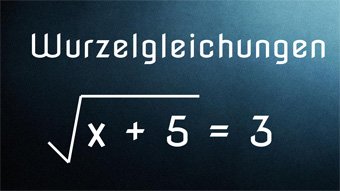Lösen wir die folgende Wurzelgleichung:
\( 3·\sqrt { x - 16 } = \sqrt { 20 + x } \)
Wir können den Vorfaktor auf der linken Seite nicht einfach entfernen. Wir quadrieren zuerst beide Seiten:
\( 3·\sqrt { x - 16 } = \sqrt { 20 + x } \quad |{ () }^{ 2 } \\ { (3·\sqrt { x - 16 } ) }^{ 2 } = { (\sqrt { 20 + x } ) }^{ 2 } \)
Wir wenden nunmehr folgendes Potenzgesetz an:
(a·b)2 = a2 · b2
Und erhalten somit:
\( 3^2·(\sqrt{ x - 16 })^2 = { (\sqrt { 20 + x } ) }^{ 2 } \\ 9·(x - 16) = 20 + x \\ 9·x - 144 = 20 + x \quad |+144 \\ 9·x = 164 + x \quad |-x \\ 8·x = 164 \quad |:8 \\ x = 20,5 \)
Als mögliches Ergebnis haben wir also x = 20,5.
Machen wir auch hier die Probe:
\( 3·\sqrt { x - 16 } = \sqrt { 20 + x } \quad |x=20,5 \\ 3·\sqrt { 20,5 - 16 } = \sqrt { 20 + 20,5 } \\ 3·\sqrt { 4,5 } = \sqrt { 40,5 } \\ 6,364 = 6,364 \)
Unser Ergebnis ist also richtig, es löst die Gleichung.