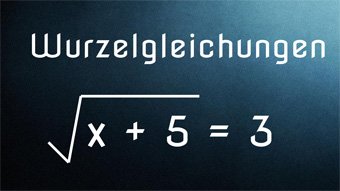Betrachten wir die Wurzelgleichung:
\( \sqrt { x + 20 } = -5 \)
Wir werden sehen, dass wir bei diesem Beispiel keine Lösung erhalten. Versuchen wir diese Gleichung zu lösen:
\( \sqrt { x + 20 } = -5 \quad |{ () }^{ 2 } \\ x + 20 = 25 \quad \quad | -20 \\ x = 5 \)
Wir erhalten also x = 5 als Lösung. Diese Lösung nennt man eine Scheinlösung.
Warum die Lösung Scheinlösung heißt, erkennen wir mit der Probe:
\( \sqrt { x + 20 } = -5 \\ \sqrt { 5 + 20 } = -5 \\ \sqrt { 25 } \neq -5 \\ 5 \neq -5 \)
Die Lösung scheint also nur richtig zu sein, ist es jedoch nicht, wie die Probe bestätigt hat.
Die Gleichung hat in Wirklichkeit keine Lösung.
Wir halten dann die leere Lösungsmenge fest mit: L = { }