Es gibt auch die Möglichkeit, Wurzelgleichungen grafisch zu lösen.
Wenn wir eine Wurzelgleichung vorzuliegen haben, können wir uns auch vorstellen, dass wir zwei Funktionsgleichungen (Linksterm = Rechtsterm) miteinander gleichgesetzt haben.
Das macht man im Allgemeinen, wenn man den Schnittpunkt zweier Funktionen bestimmen möchte. Schauen wir uns das genauer an:
\( \sqrt { 3 + x } = x + 5 \)
In diesem Beispiel wäre dann:
\( f(x) = \sqrt { 3 + x } \\ g(x) = x + 5 \)
Betrachten wir die dazugehörigen Graphen:
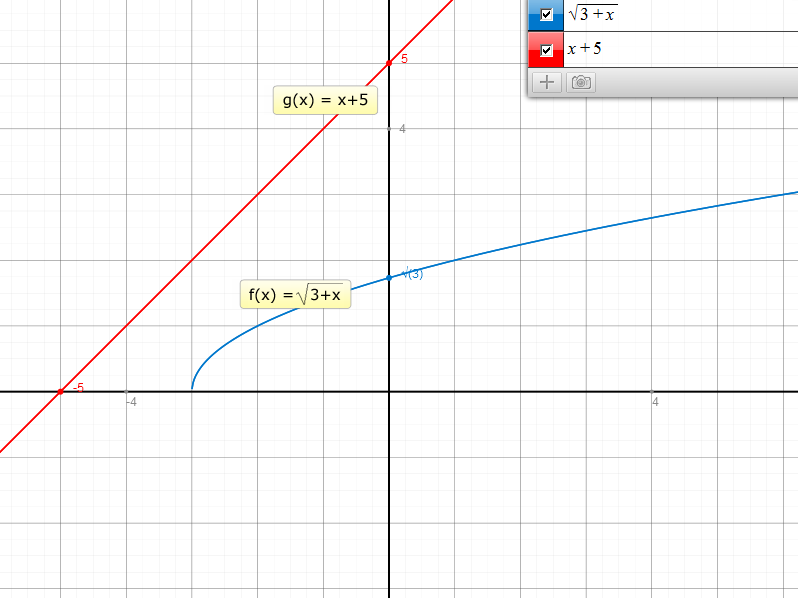
Wir sehen, dass die Funktionen keinen Schnittpunkt haben. Wenn wir die Gleichung also mit unserem Verfahren auflösen, würden wir mit der Probe erkennen, dass die Gleichung keine Lösung besitzt.
Ändern wir die Gleichung zu:
\( \sqrt { 3 + x } = x \)
Als Schnittpunktberechnung zweier Funktionen betrachtet, wäre dies:
\( f(x) = \sqrt { 3 + x } \\ g(x) = x \)
Die Graphen dazu:
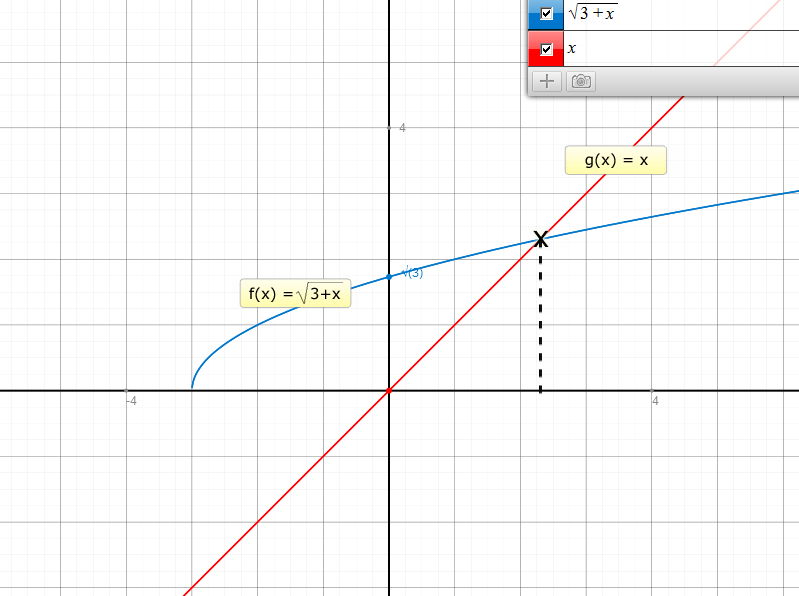
Wir sehen, dass die Graphen sich schneiden. Es muss also eine Lösung existieren. Versuchen wir abzulesen, wo diese Lösung ungefähr liegt. Sie ist bei etwa x = 2,3.
Rechnen wir nach:
\( \sqrt { 3 + x } = x \quad |{ () }^{ 2 } \\ 3 + x = { x }^{ 2 } \quad |-(3 + x) \\ { x }^{ 2 }- x - 3 = 0 \)
Wenden wir die p-q-Formel an:
\( { x }_{ 1,2 } = -(\frac { -1 }{ 2 } ) \pm \sqrt { { (\frac { -1 }{ 2 } ) }^{ 2 }-(-3) } \\ { x }_{ 1,2 } = -(\frac { -1 }{ 2 } ) \pm \sqrt { 3,25 } \)
Berechnen wir die Lösungen mit dem Taschenrechner:
x1 = 2,303
x2 = -1,303
Durch das Schaubild wissen wir, dass nur eine Lösung richtig sein kann, nämlich x = 2,303. Auch mit der Probe erhalten wir das selbe Ergebnis.