Lektion G23: Teilbarkeit und Teilbarkeitsregeln
In diesen Mathematik-Videos betrachten wir uns die Teilbarkeit für die Zahlen 0 bis 10. Wir klären, warum die Teilbarkeitsregeln funktionieren und warum die Division durch Null nicht definiert ist.
Weitere Videos für Kunden:
-
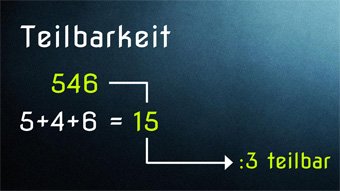
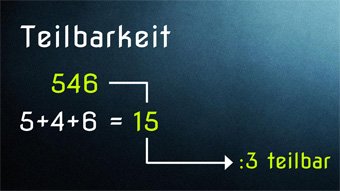
G23-1 Teilbarkeit - Regeln für Division durch 0, 1, 2, 3, 4Wieso ist die Division durch Null nicht definiert. Was ist eine Quersumme und wozu braucht man sie. Herleitung der Teilbarkeitsregeln von Eins bis Vier.
-
G23-2 Teilbarkeit - Regeln für Division durch 5 bis 10Teilbarkeitsregeln für Fünf, Sechs, Sieben, Acht, Neun, Zehn, Anwendung bei den Brüchen, Zusammenfassung aller Teilbarkeitsregeln.
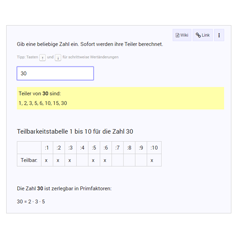
Mit diesem Mathe-Programm könnt ihr schnell und einfach die Teiler einer beliebigen Zahl bestimmen! Primzahlen werden extra hervorgehoben.
Hier findest du 10 Arbeitsblätter, mit denen du dein Wissen testen kannst.
-
AB: Lektion Teilbarkeit (Teil 1)
-
AB: Lektion Teilbarkeit (Teil 2)
-
AB: Lektion Teilbarkeit (Teil 3)
-
AB: Lektion Teilbarkeit (Teil 4)
-
AB: Lektion Teilbarkeit (Teil 5)
-
AB: Lektion Teilbarkeit (Teil 6)
-
AB: Teilbarkeitsregeln für 2, 3, 5 und 10
-
AB: Teilbarkeitsregeln für 6 und 9
-
AB: Teilbarkeitsregeln für 2, 3, 5, 6, 9 und 10
-
AB: Teilbarkeitsregeln für 4, 7 und 8
Hier findest du 3 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Teilbarkeit
- Teilbarkeit durch 1
- Teilbarkeit durch 2
- Teilbarkeit durch 3
- Teilbarkeit durch 4
- Teilbarkeit durch 5
- Teilbarkeit durch 6
- Teilbarkeit durch 7
- Teilbarkeit durch 8
- Teilbarkeit durch 9
- Teilbarkeit durch 10
- Teilbarkeit durch 11
- Teilbarkeit durch 12
- Teilbarkeit durch 13
- Teilbarkeit durch 14
- Teilbarkeit durch 15
- Teilbarkeit durch 16
- Teilbarkeit durch 17
- Teilbarkeit durch 18
- Teilbarkeit durch 19
- Teilbarkeit durch 20
- Teilbarkeit für 21 bis 30
- Division durch Null
- Null dividiert durch eine Zahl
- Zahl durch sich selbst
- Teilbarkeit über den Rest
- Schreibweise für Teilbarkeit
- Teilermenge
- Letzte Ziffern testen (Teilbarkeit durch 2, 4, 8)
- Alternierende Quersumme
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.