Allgemeinform einer quadratischen Funktion

Wir hatten uns bereits die Einführung zu den quadratischen Funktionen angeschaut sowie die Normalparabeln. Im Folgenden lernen wir die allgemeine Form bzw. „Allgemeinform“ kennen.

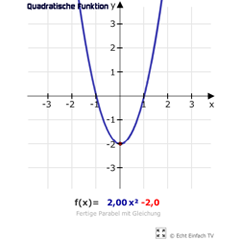
Ein Beispiel einer quadratischen Funktion in Allgemeinform wäre:

f(x) = 2·x² + 3·x + 0,5 = y

Der Graph würde wie folgt aussehen:

Parameter a

Schauen wir uns an, was eine Änderung des Koeffizienten a (der Koeffizient ist die Zahl in Multiplikation vor dem x) bei f(x) = a·x² bewirkt.

Fall: a > 0

Ist a > 0, dann sind alle Werte der Parabel größer 0, denn bei f(x) = a·x² ist für jedes x das x² positiv. Erinnert euch daran, dass eine negative Zahl ins Quadrat ebenfalls positiv wird. Da nun auch a positiv ist (mit a > 0) und wir eine Multiplikation haben, ist auch das Produkt stets positiv (oder 0). Zeichnet man diese Funktion ergibt sich eine nach oben geöffnete Parabel.

Fall: a < 0

Hier liegen die gleichen Gedanken zu Grunde. Wiederum ist x² bei f(x) = a·x² stets positiv. Nun aber ist der Vorfaktor (also der Koeffizient) negativ, was dazu führt, dass die Werte immer kleiner gleich 0 sind. Die Parabel ist also nach unten geöffnet.

Schauen wir uns den Koeffizienten a genauer an, so stellen wir fest, dass man folgende Unterscheidungen machen kann:

1. a > 1
2. a = 1
3. 0 < a < 1
4. -1 < a < 0
5. a = -1
6. a < -1

1. Fall: a > 1
Setzt man ein paar Zahlen ein, oder vergleicht den Graphen mit einer Normalparabel, dann fällt auf, dass für a > 1 die Parabel „schmaler“ wird. Man spricht auch von „in y-Richtung gestreckt“.

2. Fall: a = 1
Für a = 1 haben wir die nach oben geöffnete Normalparabel.

3. Fall: 0 < a < 1
Setzt man ein paar Zahlen ein oder vergleicht den Graphen mit einer Normalparabel, dann fällt auf, dass für 0 < a < 1 die Parabel „breiter“ wird. Man spricht auch von „in y-Richtung gestaucht“.

4. Fall: -1 < a < 0
Es ergibt sich Entsprechendes wie beim 3. Fall, nur ist die gestauchte Parabel nach unten geöffnet.

5. Fall: a = -1
Hier haben wir die nach unten geöffnete Normalparabel.

6. Fall: a < -1
Es ergibt sich Entsprechendes wie beim 1. Fall, nur ist die gestreckte Parabel nach unten geöffnet.

Die Fälle mit allen a > 0 nachstehend veranschaulicht in einem Schaubild:

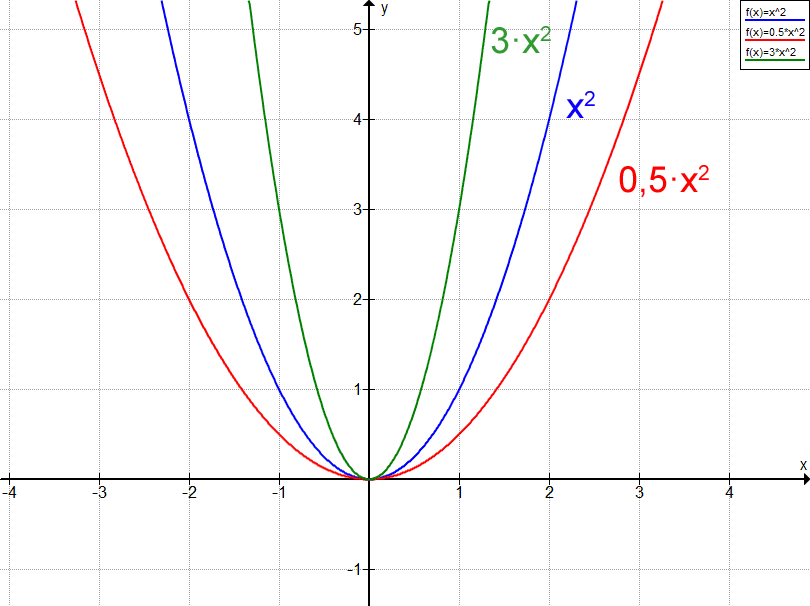
Parameter b

Der Parameter b ist bei f(x) = a·x² + b·x + c der am schwierigsten zu fassende Parameter. Er hat keine direkte Beziehung, die es sich abzulesen lohnen würde. Mit anderen Worten, verändert ihr den Parameter b, so verschiebt sich zwar die Parabel, aber die Verschiebung ist nicht so einfach wie beim Parameter c.

Parameter c

Der Parameter c ist bei f(x) = a·x² + b·x + c insofern wichtig, als dass er uns erlaubt den y-Achsenabschnitt sofort abzulesen. Zur Erinnerung: Der y-Achsenabschnitt beschreibt den Schnittpunkt mit der y-Achse, also an der Stelle x = 0. Für c > 0 haben wir demnach eine nach oben verschobene Parabel. Für c = 0 eine Parabel, die durch den Nullpunkt geht und für c < 0 haben wir eine nach unten verschobene Normalparabel.