Scheitelpunkt und Scheitelpunktform

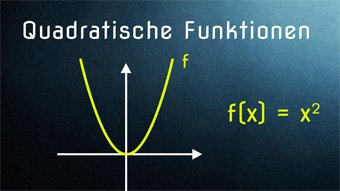
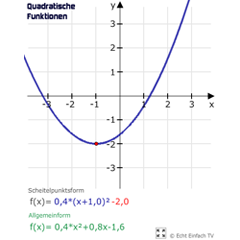
Neben der Allgemeinform f(x) = a·x² + b·x + c gibt es noch eine weitere wichtige Form einer quadratischen Funktion, und zwar die Scheitelpunktform.

Dabei muss man wissen, dass jede Parabel einen Hochpunkt bzw. einen Tiefpunkt hat. Der Hochpunkt ist der höchste Punkt der Parabel. Der Tiefpunkt ist der tiefste Punkte der Parabel.

Welcher Punkt vorliegt, kann man übrigens direkt am Vorzeichen des ersten Koeffizienten erkennen, also am a·x². Denn wenn a > 0 ist, ist die Parabel nach oben geöffnet. Sie geht also „unendlich“ weit nach oben. Für a < 0 ist die Parabel nach unten geöffnet. Sie geht „unendlich“ weit nach unten.

Diese besonderen Punkte haben auch eine besondere Bezeichnung, wir nennen sie „Scheitelpunkte“. Hat man nun die Scheitelpunktform vorzuliegen, so kann man den Scheitelpunkt direkt an dieser ablesen. Diese lautet:

f(x) = a·(x - v)² + n   → der Scheitelpunkt lautet S(v|n)

Nehmen wir uns als Beispiel die quadratische Funktion mit der Gleichung f(x) = 4·(x-3)² + 2. Hier können wir den Scheitelpunkt direkt mit S(3|2) ablesen. Wir müssen darauf, dass wir beim (x - v) ein Minus vor dem v zu stehen haben und dass wir demnach das richtige Vorzeichen bei S(v|n) wählen.

Abbildung der Beispielfunktion (eine verschobene, gestreckte Parabel):

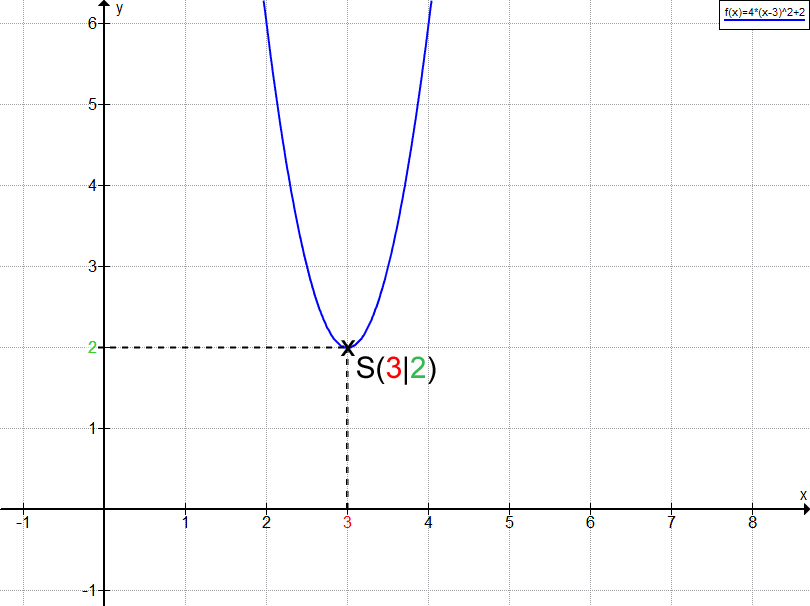
Die Funktionsgleichung lautet f(x) = 4·(x - 3)² + 2. Wir können den Scheitelpunkt ablesen mit S(3|2).

Bewege den Scheitelpunkt und stelle den Formfaktor (Stauchung/Streckung) in der folgenden Grafik ein. Erkenne dabei den Zusammenhang zwischen Koordinaten des Scheitelpunkts und der Funktionsgleichung in Scheitelpunktform:

Beachtet, dass die Variable n bei f(x) = a·(x - v)² + n nicht wie bei den linearen Funktionen den Schnittpunkt mit der y-Achse angibt, sondern die y-Koordinate des Scheitelpunktes S(v|n). Damit wir nichts verwechselen, empfehlen wir die Schreibweise mit f(x) = a·(x - S_x)² + S_y

Umwandlungen Allgemeinform ↔ Scheitelpunktform

Um von der Allgemeinform einer quadratischen Funktion auf die Scheitelpunktform zu kommen, verwendet man die quadratische Ergänzung. Allgemein:

f(x) = a·x² + b·x + c
 |
 |  Quadratische
 |  Ergänzung
 ↓
f(x) = a·(x - v)² + n

Um von der Scheitelpunktform auf die Allgemeinform zu kommen, multiplizieren wir einfach mit Hilfe der binomischen Formeln aus und fassen zusammen. Allgemein:

f(x) = a·(x - v)² + n
 |
 |  Ausmultiplizieren
 ↓
f(x) = a·x² + b·x + c

Beispiel:

f(x) = 5·(x - 3)² + 7
f(x) = 5·(x² - 2·3·x + 3²) + 7
f(x) = 5·x² - 5·6·x + 5·9 + 7
f(x) = 5·x² - 30·x + 52