Wir können die Normalparabel, die durch die Gleichung f(x) = x² entsteht auch verschieben (nach oben bzw. unten). Hierzu addieren wir einfach einen Wert auf das x² hinauf.
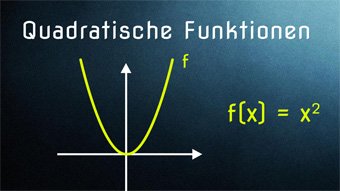
Die Normalparabel ohne Verschiebung sieht so aus:
Bei der folgenden Grafik könnt ihr den Parabel verschieben und sehen, wie sich ihre Funktionsgleichung ändert:
Den Punkt im Koordinatenursprung (den ihr in der Grafik oben verschieben könnt) nennen wir „Scheitelpunkt“.
Schieben wir den Scheitelpunkt beispielsweise um +2 nach oben, so lautet unsere Funktionsgleichung: f(x) = x² + 2
Schieben wir den Scheitelpunkt beispielsweise um -1 nach unten, so lautet unsere Funktionsgleichung: f(x) = x² - 1
Der Wert der Verschiebung wird stets bei der Funktionsgleichung als Addition berücksichtigt.
Schieben wir den Scheitelpunkt übrigens in den Koordinatenursprung, so addieren wir +0 hinauf, dass heißt unsere Funktionsgleichung lautet: f(x) = x² + 0 = x² (die Normalparabel).
Wertetabelle der verschobenen Normalparabel
Die Wertetabelle zeigt die x-Werte von -4 bis +4. Wenn wir eine Verschiebung haben (nachfolgend um +2 nach oben), so müssen wir diese wie folgt berücksichtigen:
| x | x²+2 | Punkt |
|---|---|---|
| -4 | 16+2 | P(-4|18) |
| -3 | 9+2 | P(-3|11) |
| -2 | 4+2 | P(-2|6) |
| -1 | 1+2 | P(-1|3) |
| 0 | 0+2 | P(0|2) |
| 1 | 1+2 | P(1|3) |
| 2 | 4+2 | P(2|6) |
| 3 | 9+2 | P(3|11) |
| 4 | 16+2 | P(4|18) |