Lektion GEO02: Kreis und Winkel
In den folgenden Videos erfahrt ihr alles Wesentliche, was ihr über Kreise und Winkel wissen müsst.
Dies ist übrigens ein wesentlicher Wissensbaustein zum Verständnis der Trigonometrie.
Kreis und Winkel - Der Kreis
Der Kreis: Entstehung und Definition des Kreises über Punkte und Polygon. Aufbau des Kreises, Elemente des Kreises. Bedeutung der Kreiszahl Pi. Berechnen von Kreisfläche und Kreisumfang.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
GEO02-2 Kreis und Winkel - WinkelWinkel: Entstehung von Winkeln durch Drehung zweier Strahlen, Winkelmaße (Prozent, Grad, Bogenmaß), Winkelmessung mit dem Geo-Dreieck. Winkelarten und Winkelbezeichnungen. Winkel unter 0 Grad und über 360 Grad.
-
GEO02-3 Kreis und Winkel - Winkel an GeradenWinkel an zwei sich schneidenden Gerade. Gegenwinkel (Scheitelwinkel) und Nebenwinkel, Eigenschaften. Winkel an Parallelen: Stufen- und Wechselwinkel. Zusammenfassung.
-
 WinkelartenNullwinkel, spitzer Winkel, rechter Winkel, stumpfer Winkel, gestreckter Winkel, überstumpfer Winkel und Vollwinkel.
WinkelartenNullwinkel, spitzer Winkel, rechter Winkel, stumpfer Winkel, gestreckter Winkel, überstumpfer Winkel und Vollwinkel. -
 Kreisentstehung (Punkte)Mit diesem Programm lässt sich darstellen, wie ein Kreis aus unendlich vielen Punkten entsteht.
Kreisentstehung (Punkte)Mit diesem Programm lässt sich darstellen, wie ein Kreis aus unendlich vielen Punkten entsteht. -
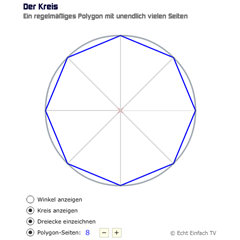 Kreisentstehung (Polygon)Hier lässt sich zeigen, wie ein Kreis als regelmäßiges Polygon mit unendlich vielen Seiten beschrieben werden kann.
Kreisentstehung (Polygon)Hier lässt sich zeigen, wie ein Kreis als regelmäßiges Polygon mit unendlich vielen Seiten beschrieben werden kann. -
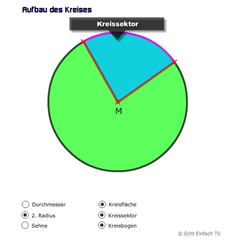 Kreis: Aufbau des KreisesBei diesem Programm sind alle Elemente des Kreises aktivierbar. Sehr praktisch, um den Aufbau des Kreises zu lernen.
Kreis: Aufbau des KreisesBei diesem Programm sind alle Elemente des Kreises aktivierbar. Sehr praktisch, um den Aufbau des Kreises zu lernen. -
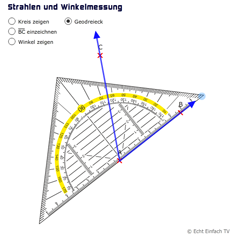 Strahlen und Winkelmessung (Geodreieck)Hier können zwei Strahlen beliebig voneinander weggedreht werden. Anschließend kann man mit einem Geodreieck den Winkel abmessen!
Strahlen und Winkelmessung (Geodreieck)Hier können zwei Strahlen beliebig voneinander weggedreht werden. Anschließend kann man mit einem Geodreieck den Winkel abmessen! -
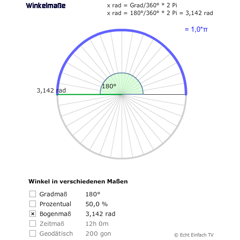 Winkelmaße (Gradmaß, Prozent, Bogenmaß)Verschiedene Winkelmaße (Grad, Prozent, Bogenmaß, Gon, Zeit) zur Veranschaulichung am Kreis.
Winkelmaße (Gradmaß, Prozent, Bogenmaß)Verschiedene Winkelmaße (Grad, Prozent, Bogenmaß, Gon, Zeit) zur Veranschaulichung am Kreis. -
 Winkelnamen (Griechische Buchstaben)Alle griechischen Buchstaben (Klein- und Großschreibung) inklusive Lernmodus!
Winkelnamen (Griechische Buchstaben)Alle griechischen Buchstaben (Klein- und Großschreibung) inklusive Lernmodus! -
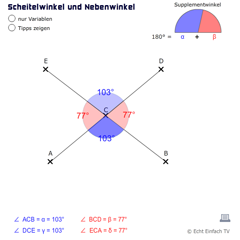 Winkel: Scheitelwinkel und NebenwinkelHier schneiden sich zwei Geraden und es entstehen 4 Winkel. Die Punkte der Geraden lassen sich bei diesem Programm bewegen, so dass beliebige Winkel entstehen können.
Winkel: Scheitelwinkel und NebenwinkelHier schneiden sich zwei Geraden und es entstehen 4 Winkel. Die Punkte der Geraden lassen sich bei diesem Programm bewegen, so dass beliebige Winkel entstehen können. -
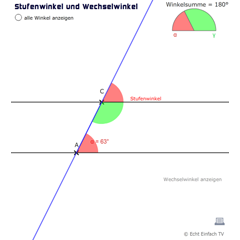 Winkel: Stufenwinkel und WechselwinkelZwei Punkte auf zwei Parallelen können frei bewegt werden. Dabei werden Zusammenhänge zwischen Stufenwinkel und Wechselwinkel erkennbar!
Winkel: Stufenwinkel und WechselwinkelZwei Punkte auf zwei Parallelen können frei bewegt werden. Dabei werden Zusammenhänge zwischen Stufenwinkel und Wechselwinkel erkennbar! -
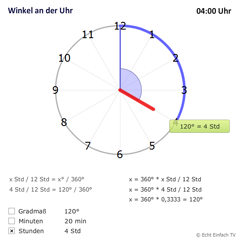 Winkel an der UhrMit diesem Programm könnt ihr Winkel an der Uhr üben. Wählt euch Minuten oder Stunden und stellt die Uhrzeit ein. Ein Winkel ergibt sich.
Winkel an der UhrMit diesem Programm könnt ihr Winkel an der Uhr üben. Wählt euch Minuten oder Stunden und stellt die Uhrzeit ein. Ein Winkel ergibt sich. -
 Kreisrechner: Kreis berechnenEinfach einen Wert eingeben, alle Ergebnisse werden ausgerechnet für Radius, Durchmesser, Umfang, Flächeninhalt, Winkel, Kreisbogen, Kreissektor und Sehne.
Kreisrechner: Kreis berechnenEinfach einen Wert eingeben, alle Ergebnisse werden ausgerechnet für Radius, Durchmesser, Umfang, Flächeninhalt, Winkel, Kreisbogen, Kreissektor und Sehne.
Hier findest du 6 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 7 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Kreis - Definition und Merkmale
- Kreis - Wortherkunft und andere Sprachen
- Kreise im Alltag
- Kreis - Formelübersicht
- Kreislinie
- Kreis: Radius
- Kreis: Durchmesser
- Kreisfläche
- Kreis: Sehne
- Kreisbogen
- Kreissektor (Kreisausschnitt)
- Kreissegment (Kreisabschnitt)
- Linien an Kreisen
- Symmetrie des Kreises
- Winkel - Einführung
- Winkelarten
- Nullwinkel (α = 0°)
- Spitzer Winkel (0° < α < 90°)
- Rechter Winkel (α = 90°)
- Stumpfer Winkel (90° < α < 180°)
- Gestreckter Winkel (α = 180°)
- Überstumpfer Winkel (180° < α < 360°)
- Vollwinkel (α = 360°)
- Winkel an parallelen Geraden
- Scheitelwinkel/Gegenwinkel
- Nebenwinkel
- Stufenwinkel
- Wechselwinkel
- Winkelmaß
- Winkel umrechnen: Grad zu Bogenmaß
- Griechische Winkelnamen (α, β, γ, …)
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.


