Lektion G26: Lineare Gleichungen, Quadratische Gleichungen
Wir betrachten uns zuerst die linearen Gleichungen. Wie sie aufgebaut sind und wir sie lösen können.
Dann schauen wir uns an, was der Unterschied zwischen Gleichung und Funktion ist.
Danach klären wir, was eine quadratische Gleichung ist, wie diese Art von Gleichungen aufgebaut ist und mit welchen Lösungsverfahren wir sie lösen können.
Quadratische Gleichungen - Einführung
Was sind Quadratische Gleichungen, Allgemeinform und Normalform, Quadratisches Glied, Lineares Glied, Absolutes Glied, Koeffizienten, Lösen einer quadratischen Gleichung mit Hilfe der p-q-Formel, Lösen der Gleichung mittels Deutung als Funktion.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G26-1 Lineare Gleichungen - EinführungEinführung zu den linearen Gleichungen. Lösen von linearen Gleichungen mittels Äquivalenzumformung und per Deutung als Funktionen. Lösungsmengen.
-
G26-2 Unterschied zwischen Gleichung und FunktionUnterschied zwischen Gleichung und Funktion. Speziell quadratische Gleichungen und quadratische Funktionen.
-
G26-4 Quadratische Gleichungen - Herleitung p-q-FormelHerleitung der p-q-Formel, weitere Lösungsverfahren für quadratische Gleichungen (Wurzeln, Ausklammern, Linearfaktoren), Grafisches Lösen von quadratischen Gleichungen.
-
G26-5 Quadratische Gleichungen - abc-FormelHerleitung der abc-Formel (große Lösungsformel bzw. Mitternachtsformel), Lösen Quadratischer Gleichungen mit abc-Formel, Zusammenfassung des neuen Wissens.
Im Folgenden findet ihr Programme zu den quadratischen Gleichungen, die euch helfen, die Lösungen eurer Hausaufgaben zu kontrollieren.
-
 Quadratische Gleichungen und p-q-FormelDieses Programm löst beliebige quadratische Gleichungen mit Hilfe der p-q-Formel, inklusive Rechenweg.
Quadratische Gleichungen und p-q-FormelDieses Programm löst beliebige quadratische Gleichungen mit Hilfe der p-q-Formel, inklusive Rechenweg. -
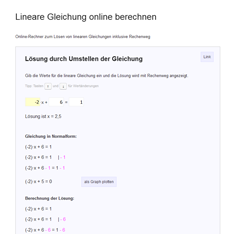 Lineare Gleichung berechnenDie Lösung der linearen Gleichung wird euch komplett mit Rechenweg angezeigt (Umstellen der Gleichung).
Lineare Gleichung berechnenDie Lösung der linearen Gleichung wird euch komplett mit Rechenweg angezeigt (Umstellen der Gleichung). -
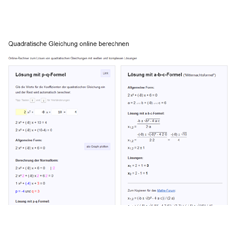 Quadratische Gleichung RechnerDie Lösung wird euch komplett mit Rechenweg angezeigt. Zum einen mit p-q-Formel und zum anderen mit abc-Formel, sog. Mitternachtsformel.
Quadratische Gleichung RechnerDie Lösung wird euch komplett mit Rechenweg angezeigt. Zum einen mit p-q-Formel und zum anderen mit abc-Formel, sog. Mitternachtsformel.
Hier findest du 5 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 6 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Lineare Gleichungen
- Lösen von linearen Gleichungen
- Formen von linearen Gleichungen
- Lineare Gleichungen ohne Lösung
- Lineare Gleichungen mit unendlich vielen Lösungen
- Quadratische Gleichungen - Einführung
- Verfahren zum Lösen von Quadratischen Gleichungen
- abc-Formel (Mitternachtsformel)
- Herleitung der abc-Formel (Mitternachtsformel)
- p-q-Formel
- Herleitung der p-q-Formel
- Quadratische Gleichungen lösen mit Binomischen Formeln
- Quadratische Gleichungen lösen durch Ausklammern
- Quadratische Gleichungen lösen durch Wurzelziehen
- Gemischtquadratische Gleichungen
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.




