Die Berechnung der Länge eines Weges längs eines vorgegebenen Funktiosverlaufes beruht auf der Summation von Wegstücken längs dieser Kurve. Dabei werden die kleinen, aber endlich großen Wegstücke Δs durch den Grenzübergang Δs → 0 in unendlich kleine Wegelemente ds überführt.
Damit erfolgt die Berechnung der Gesamtlänge einfach durch Integration aller Teilstücke:
\( S = \int\limits_{ {x_1} }^{ {x_2} } {ds} \) Gl. 161
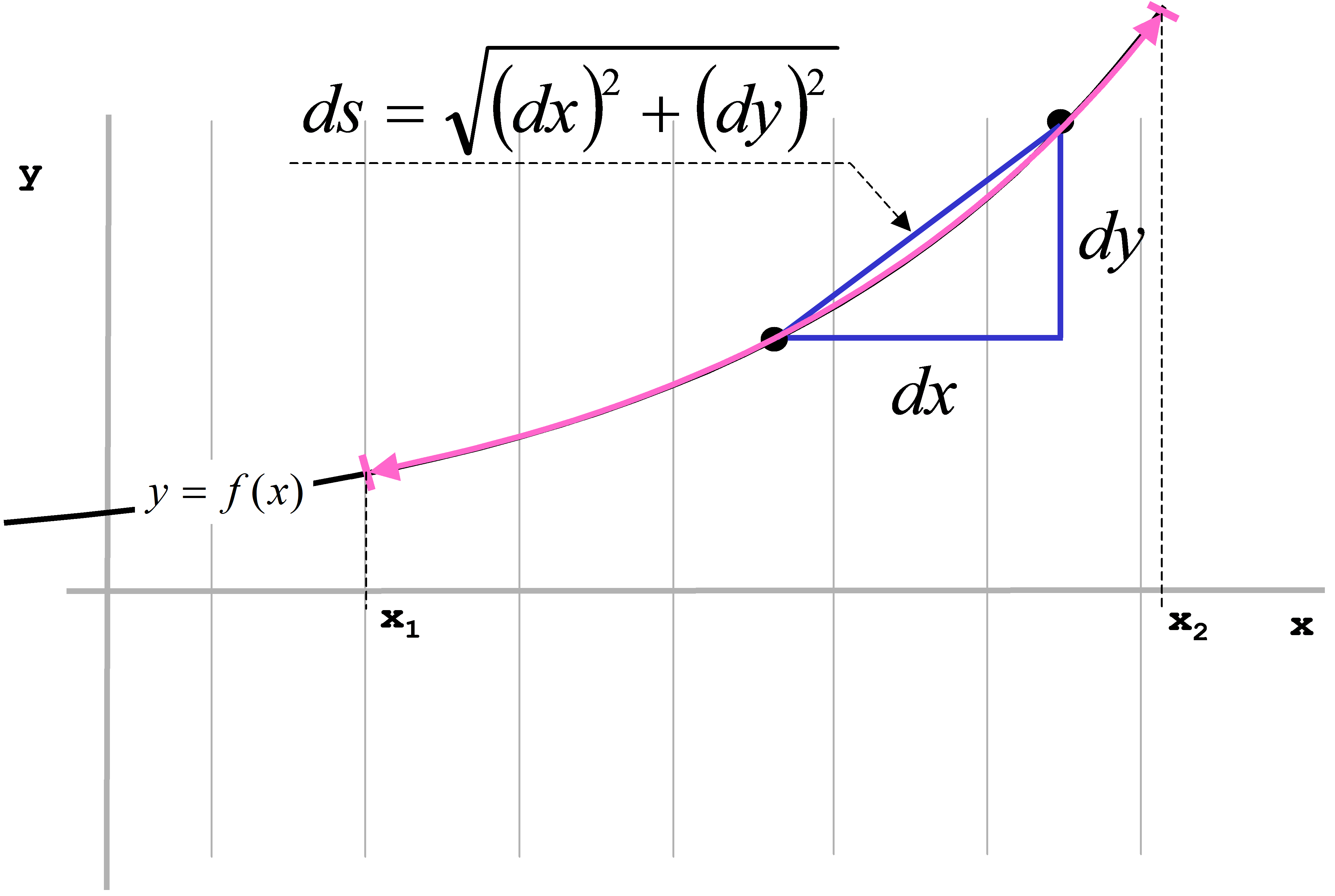
Nun kann aber das Wegstück ds durch Anwendung des Satzes von Pythagoras auf die Elemente dx und dy zurückgeführt werden (Abbildung 24).
Das infinitesimal kleine Bogenelement Δs ergibt sich zu:
\( ds = \sqrt { { {\left( {dx} \right)}^2} + { {\left( {dy} \right)}^2} } \) Gl. 162
einsetzen in Gl. 161:
\( S = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt { { {\left( {dx} \right)}^2} + { {\left( {dy} \right)}^2} } = } \int\limits_{ {x_1} }^{ {x_2} } {\sqrt {1 + { {\left( {\frac{ {dy} }{ {dx} } } \right)}^2} } dx = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt {1 + { {\left( {y'\left( x \right)} \right)}^2} } dx} } \) Gl. 163
ergibt die Berechnungsvorschrift für die Weglänge.
Beispiel 1:
Es sei die Bogenlänge eines Kreissegments von x=-R bis x=R zu berechnen.
Für dieses Kreissegment gilt die Beziehung:
\(y = \sqrt { {R^2} - {x^2} } \) wobei R der Radius des Kreises ist.
erste Ableitung:
\(y' = \frac{1}{ {2 \cdot \sqrt { {R^2} - {x^2} } } } \cdot \left( { - 2x} \right) = - \frac{x}{ {\sqrt { {R^2} - {x^2} } } }\)
in Gl. 163 einsetzen
\(S = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt {1 + { {\left( {y'\left( x \right)} \right)}^2} } dx} = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt {1 + \frac{ { {x^2} } }{ { {R^2} - {x^2} } } } dx} = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt {\frac{ { {R^2} } }{ { {R^2} - {x^2} } } } dx} \)
und umformen:
\( S = \int\limits_{ {x_1} }^{ {x_2} } {\sqrt{\frac{ { {R^2} } }{ { {R^2} - {x^2} } } } dx = } \int\limits_{ {x_1} }^{ {x_2} } {\frac{1}{ {\sqrt {1 - { {\left({\frac{x}{R} } \right)}^2} } } }dx \text{ mit } z = \frac{x}{R} \quad \Rightarrow \quad dx = R \cdot dz} \)
das Integral ist nach Substitution elementar lösbar:
\( S = R\int\limits_{ {x_1} }^{ {x_2} } {\frac{1}{ {\sqrt {1 - { {\left( z \right)}^2} } } }dz = R \cdot } \left. {\arcsin \left( z \right)} \right|_{z = - 1}^{z = 1} = R \cdot \left( {\frac{\pi }{2} + \frac{\pi }{2} } \right) = R \cdot \pi \)
Bisweilen ist es einfacher, die Integration in einer alternativen Darstellung der Kurve vorzunehmen:
Beispiel 2:
Berechnung der Bogenlänge eines Kreissegments in Polarkoordinaten.
Für dieses Kreissegment gilt die Beziehung:
\(y = R \cdot \sin \phi ; x = R \cdot \cos \phi \) wobei R der Radius des Kreises ist.
erste Ableitung:
\(\frac{ {dy} }{ {d\phi } } = R \cdot \cos \phi ; \frac{ {dx} }{ {d\phi } } = - R \cdot \sin \phi \)
in Gl. 163
\(S = \int\limits_{ {\phi _1} }^{ {\phi _2} } {\sqrt { { {\left({dx} \right)}^2} + { {\left( {dy} \right)}^2} } = } \int\limits_{ {\phi _1} }^{ {\phi _2} } {\sqrt { { {\left( {R \cdot \cos \phi } \right)}^2} + { {\left( { - R \cdot \sin \phi } \right)}^2} } \cdot d\phi = } R \cdot \int\limits_{ {\phi _1} }^{ {\phi _2} } {\sqrt { { {\cos }^2}\phi + { {\sin }^2}\phi } } \cdot d\phi \)
da \({\cos ^2}\phi + {\sin ^2}\phi = 1\)
vereinfacht sich der Integrand:
\( S = R \cdot \int\limits_{ {\phi _1} }^{ {\phi _2} } 1 \cdot d\phi = \left. {R \cdot \phi } \right|_{ {\phi _1} }^{ {\phi_2} } \)
für einen Vollkreis mit j=2p ergibt sich die Bogenlänge zu:
\(S = 2R \cdot \pi \)
was ja dem Umfang eines Kreises entspricht.
