Wegen der Mehrdeutigkeit der sog. unbestimmten Integrale, also der Integrale, die nicht auf bestimmte Anfangs- oder Endwerte festgelegt sind, wird die Konstante C bei der Lösung unbestimmter Integrale als Ausdruck der Lösungsvielfalt hinzugesetzt. Anders bei den bestimmten Integralen. Bestimmte Integrale zeichnen sich durch die Angabe von Anfangs- und Endwert im Integrationszeichen aus:
\( F = \int\limits_{ {x_1} }^{ {x_2} } {f(x)} dx\, = F({x_2}) + C - \left( {F({x_1}) + C} \right) = F({x_2}) - F({x_1}) \) Gl. 134
oder abgekürzt:
\( F = \int\limits_{ {x_1} }^{ {x_2} } {f(x)} dx\, = \left. {F(x)} \right|_{ {x_1} }^{ {x_2} } = F({x_2}) - F({x_1}) \) Gl. 135
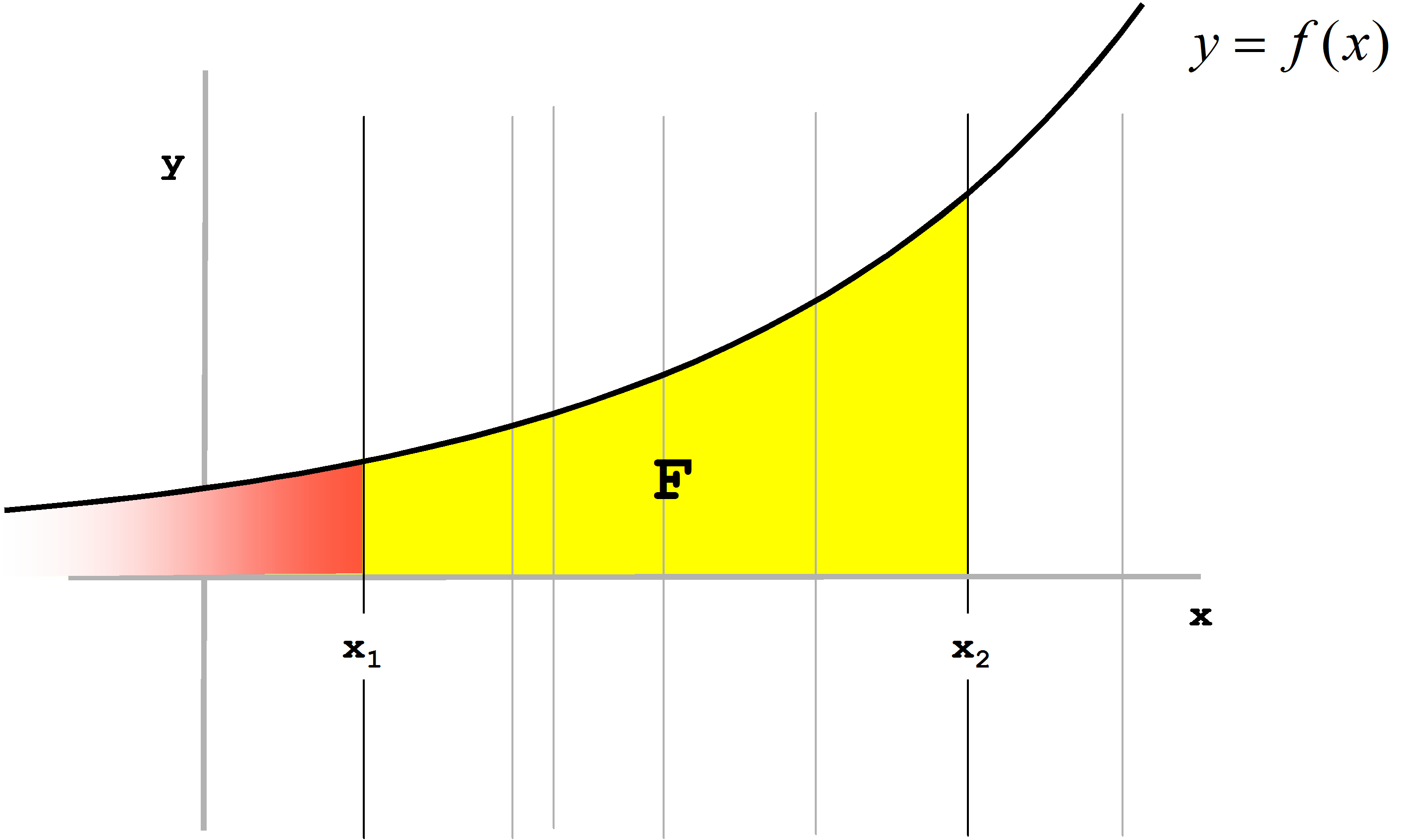
Sein Wert ist durch die Differenz der Integrale aus Endwert F(x2) und Anfangswert F(x1) gegeben (Gl. 134). Durch diese Operation wird der unbestimmte Ausdruck F(x) zu einer konkreten, d.h. bestimmten Fläche F, die unbestimmte Konstante C verschwindet. Abbildung 20 verdeutlicht die Berechnung der konkreten Fläche, also des bestimmten Integrals durch die Differenzbildung.
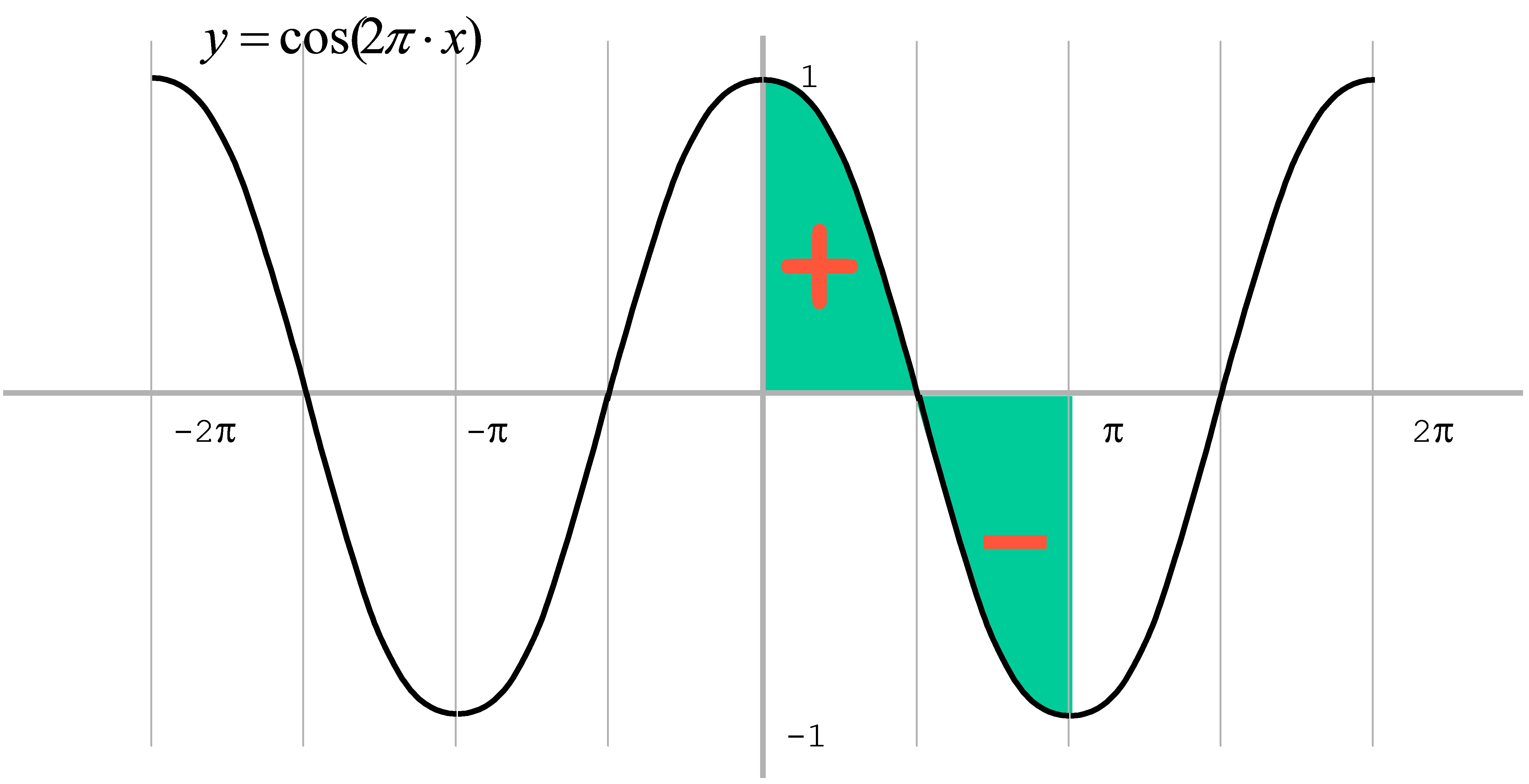
Andererseits ist bei der Flächenberechnung zu beachten, dass es positive, aber auch negative Flächen gibt. Veranschaulicht man sich noch einmal das Prinzip der Integration (Abbildung 18), wird deutlich, dass negative Funktionswerte zu negativen Flächen führen (Abbildung 21). Soll also die Absolutfläche unter einer Kurve berechnet werden, die Nulldurchgänge aufweist, so ist die Ausführung der bestimmten Integration abschnittsweise durchzuführen.
Die Integrationsgrenzen der Abschnitte sind dann entsprechend der Nulldurchgänge zu wählen:
\( F = \int\limits_{ {x_1} }^{ {x_2} } {f(x)} dx\, = \left| {\left. {F(x)} \right|_{ {x_1} }^{ {x_0} } } \right| + \left| {\left. {F(x)} \right|_{ {x_0} }^{ {x_2} } } \right|\,\,... \) Gl. 136
Beispiel:
Gesucht ist die Fläche unter der Cosinus-Kurve \(f(x) = \cos (2\pi x)\) in den Grenzen von x = 0 bis x = π.
Lösung:
\( F = \left| {\int\limits_0^{\frac{\pi }{2} } {\cos (2\pi \cdot x)} dx} \right| + \left| {\int\limits_{\frac{\pi}{2} }^\pi {\cos (2\pi \cdot x)} dx} \right| \)
\( F = \left| {\frac{1}{ {2\pi } }\left( { - \sin \left( {2\pi \cdot x} \right)} \right)} \right|_0^{\frac{\pi }{2} } + \left| {\frac{1}{ {2\pi } }\left( { - \sin \left( {2\pi \cdot x} \right)} \right)} \right|_{\frac{\pi }{2} }^\pi = \frac{1}{\pi } \)
