Bezierkurven

Bezierkurven sind jedem, der Vektorgrafiken erstellt, bekannt. Eine Bezierkurve in ihrer gebräuchlichsten Form verbindet zwei Punkte, einen Anfangs- und einen Endpunkt, mir einer in gewissen Grenzen frei formbaren Linie. Mit zwei weiteren Punkten, den sog. Kontrollpunkten, ist die Form der Linie steuerbar. Im Gebrauch werden die Kontrollpunkte mit dem Start- oder Endpunkt durch Geraden verbunden. Dabei zeigt sich, dass die Richtung dieser Kontrollgeraden mit der Tangente der Bezierkurve in Start- oder Endpunkt übereinstimmt. Die Länge der Gerade bestimmt hingegen den Kurvenverlauf zwischen den Endpunkten. Was verbirgt sich aber aus mathematischer Sicht hinter einer Bezierkurve?

Abbildung 14

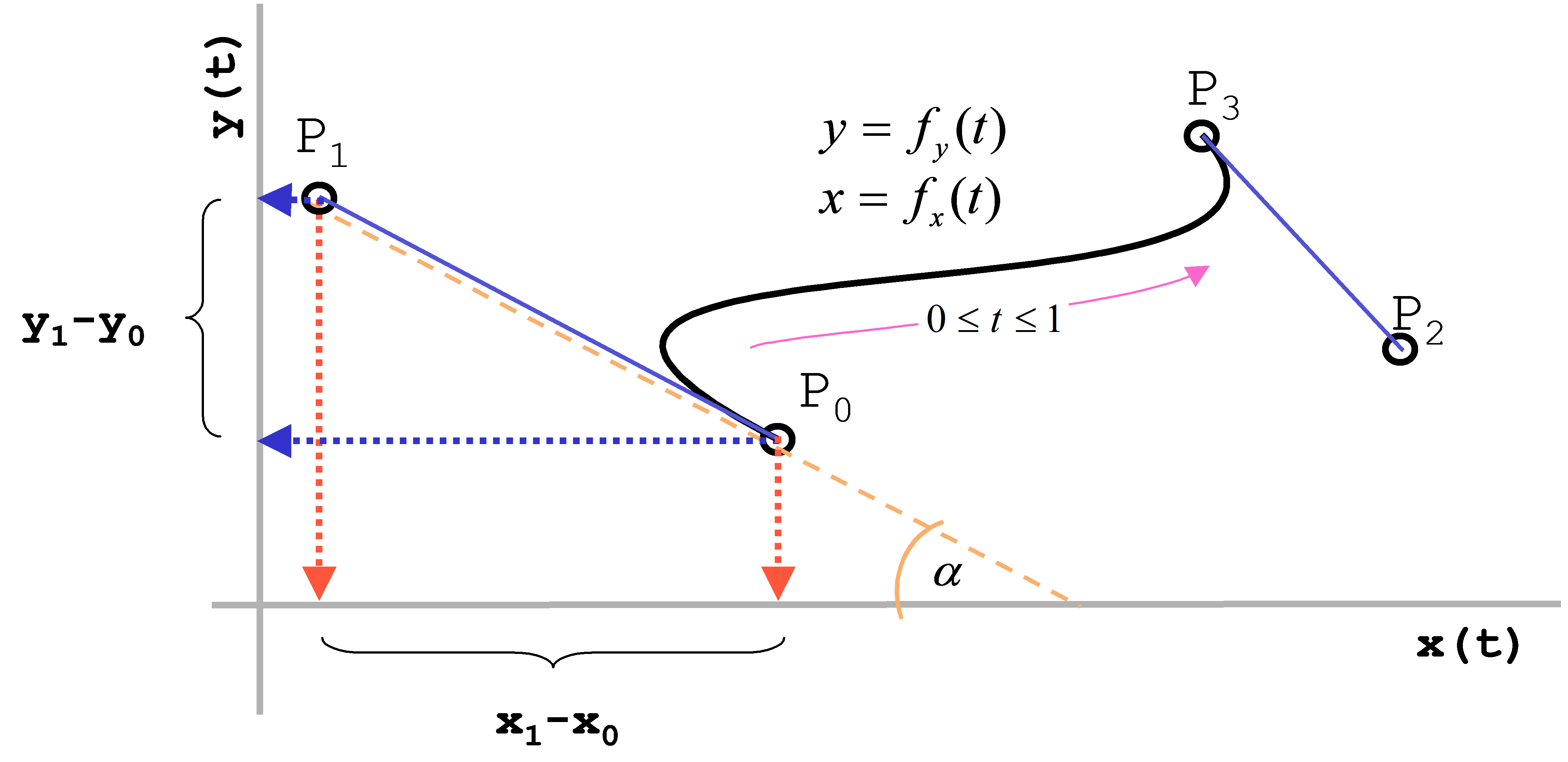
In Abbildung 14 ist der Punkt P₀ der Start-, P₃ der Endpunkt. Die Punkte P₁ und P₂ sind die Steuerpunkte. Die Kurve selbst wird durch zwei parametrisierte kubische Funktionen für x und y dargestellt:

\( x(t) = {x_0} \cdot {u_0} \cdot {\left( {1 - t} \right)^3} + {x_1} \cdot {u_1} \cdot t \cdot {\left( {1 - t} \right)^2} + {x_2} \cdot {u_2} \cdot {t^2} \cdot \left( {1 - t} \right) + {x_3} \cdot {u_3} \cdot {t^3} \) Gl. 86

\( y(t) = {y_0} \cdot {v_0} \cdot {\left( {1 - t} \right)^3} + {y_1} \cdot {v_1} \cdot t \cdot {\left( {1 - t} \right)^2} + {y_2} \cdot {v_2} \cdot {t^2} \cdot \left( {1 - t} \right) + {y_3} \cdot {v_3} \cdot {t^3} \) Gl. 87

worin die x_i und y_i (i = 0, 1, 2, 3) die Koordinaten der vier beschreibenden Punkte darstellen. Die u_i und v_i hingegen sind Gewichte, die geeignet zu wählen sind. Der sichtbare Funktionsverlauf entsteht durch die übliche Darstellung der Funktionswerte von y und x in einem kartesischen Koordinatensystem.

\( y(x) = y(x(t)) \) Gl. 88

Die Bedeutung des Parameters 0 ≤ t ≤ 1 wird deutlich, wenn die Funktion an ihren Rändern (t=0 bzw. t=1) betrachtet wird. Dann ist zu erkennen, dass der Einfluss des jeweils anderen Punktpaares ausgeschlossen ist und die Funktionswerte mit den Koordinaten der jeweiligen Punkte übereinstimmen, wenn die Gewichte u₀ und u₃ bzw. v₀ und v₃ gleich 1 gewählt werden:

\( x(0) = {x_0} \text{ und } x(1) = {x_3} \) Gl. 89

\( y(0) = {y_0} \text{ und } y(1) = {y_3} \) Gl. 90

Mit dieser Randwert-Betrachtung konnten die Werte für die Gewichteu₀, u₃, v₀,v₃ bestimmt werden. Wie aber sind die Gewichteu₁, u₂, v₁, v₂ zu bestimmen? Hier kommt nun die Forderung ins Spiel, dass die Richtung der Steuergeraden mit der Tangente der Kurve im jeweiligen Endpunkt übereinstimmen soll:

\( \frac{ {dy(x(t = 0))} }{ {dx} } = \frac{ { {y_1} - {y_0} } }{ { {x_1} - {x_0} } } \) Gl. 91

bzw.

\( \frac{ {dy(x(t = 1))} }{ {dx} } = \frac{ { {y_2} - {y_3} } }{ { {x_2} - {x_3} } } \) Gl. 92

Nun kann die Gl. 87 nicht direkt nach dx abgeleitet werden, da sie ja keine Funktion von x darstellt.

Daher werden sowohl Gl. 87 als auch Gl. 88 nach dt abgeleitet und entsprechend

\( \frac{ {dy} }{ {dx} } = \frac{ {dy} }{ {dt} } \cdot \frac{ {dt} }{ {dx} } \) Gl. 93

zum gesuchten Differenzialquotienten kombiniert.

Mit

\( \frac{ {dx(t)} }{ {dt} } = - {x_0} \cdot 3{\left( {1 - t} \right)^2} + {x_1} \cdot {u_1} \cdot \left[ { { {\left( {1 - t} \right)}^2} - 2t\left( {1 - t} \right)} \right] + {x_2} \cdot {u_2} \cdot \left[ {2t \cdot \left( {1 - t} \right) - {t^2} } \right] + {x_3} \cdot 3{t^2} \) Gl. 94

\( \frac{ {dy(t)} }{ {dt} } = - {y_0} \cdot 3{\left( {1 - t} \right)^2} + {y_1} \cdot {v_1} \cdot \left[ { { {\left( {1 - t} \right)}^2} - 2t\left( {1 - t} \right)} \right] + {y_2} \cdot {v_2} \cdot \left[ {2t \cdot \left( {1 - t} \right) - {t^2} } \right] + {y_3} \cdot 3{t^2} \) Gl. 95

wird Gl. 115 zu

\( \frac{ {dy} }{ {dx} } = \frac{ { - {y_0} \cdot 3{ {\left( {1 - t} \right)}^2} + {y_1} \cdot {v_1} \cdot \left[ { { {\left( {1 - t} \right)}^2} - 2t\left( {1 - t} \right)} \right] + {y_2} \cdot {v_2} \cdot \left[ {2t \cdot \left( {1 - t} \right) - {t^2} } \right] + {y_3} \cdot 3{t^2} } }{ { - {x_0} \cdot 3{ {\left( {1 - t} \right)}^2} + {x_1} \cdot {u_1} \cdot \left[ { { {\left( {1 - t} \right)}^2} - 2t\left( {1 - t} \right)} \right] + {x_2} \cdot {u_2} \cdot \left[ {2t \cdot \left( {1 - t} \right) - {t^2} } \right] + {x_3} \cdot 3{t^2} } } \) Gl. 96

Nunmehr erfolgt der Vergleich mit den Bedingungen von Gl. 91 und Gl. 92:

\( {\left. {\frac{ {dy} }{ {dx} } } \right|_{t = 0} } = \frac{ { - {y_0} \cdot 3 + {y_1} \cdot {v_1} } }{ { - {x_0} \cdot 3 + {x_1} \cdot {u_1} } } = \frac{ { {y_1} - {y_0} } }{ { {x_1} - {x_0} } } \) Gl. 97

bzw.

\( {\left. {\frac{ {dy} }{ {dx} } } \right|_{t = 1} } = \frac{ { - {y_2} \cdot {v_2} + {y_3} \cdot 3} }{ { - {x_2} \cdot {u_2} + {x_3} \cdot 3} } = \frac{ { {y_2} - {y_3} } }{ { {x_2} - {x_3} } } \) Gl. 98

Die geforderte Gleichheit ist nur zu erfüllen, wenn u₁,u₂, v₁, v₂ = 3 sind. Damit sind nun alle Elemente der Bezierkurve gefunden und die Gleichungen lauten nunmehr:

\( x(t) = {x_0} \cdot {\left( {1 - t} \right)^3} + {x_1} \cdot 3t \cdot {\left( {1 - t} \right)^2} + {x_2} \cdot 3{t^2} \cdot \left( {1 - t} \right) + {x_3} \cdot {t^3} \) Gl. 99

\( y(t) = {y_0} \cdot {\left( {1 - t} \right)^3} + {y_1} \cdot 3t \cdot {\left( {1 - t} \right)^2} + {y_2} \cdot 3{t^2} \cdot \left( {1 - t} \right) + {y_3} \cdot {t^3} \) Gl. 100