Eine der wichtigsten Anwendungen der Differenziation ist die Bestimmung von Extremwerten.
Extremwerte zeichnen sich dadurch aus, dass die Funktion genau an diesen Stellen verschwindende Steigungen aufweisen:
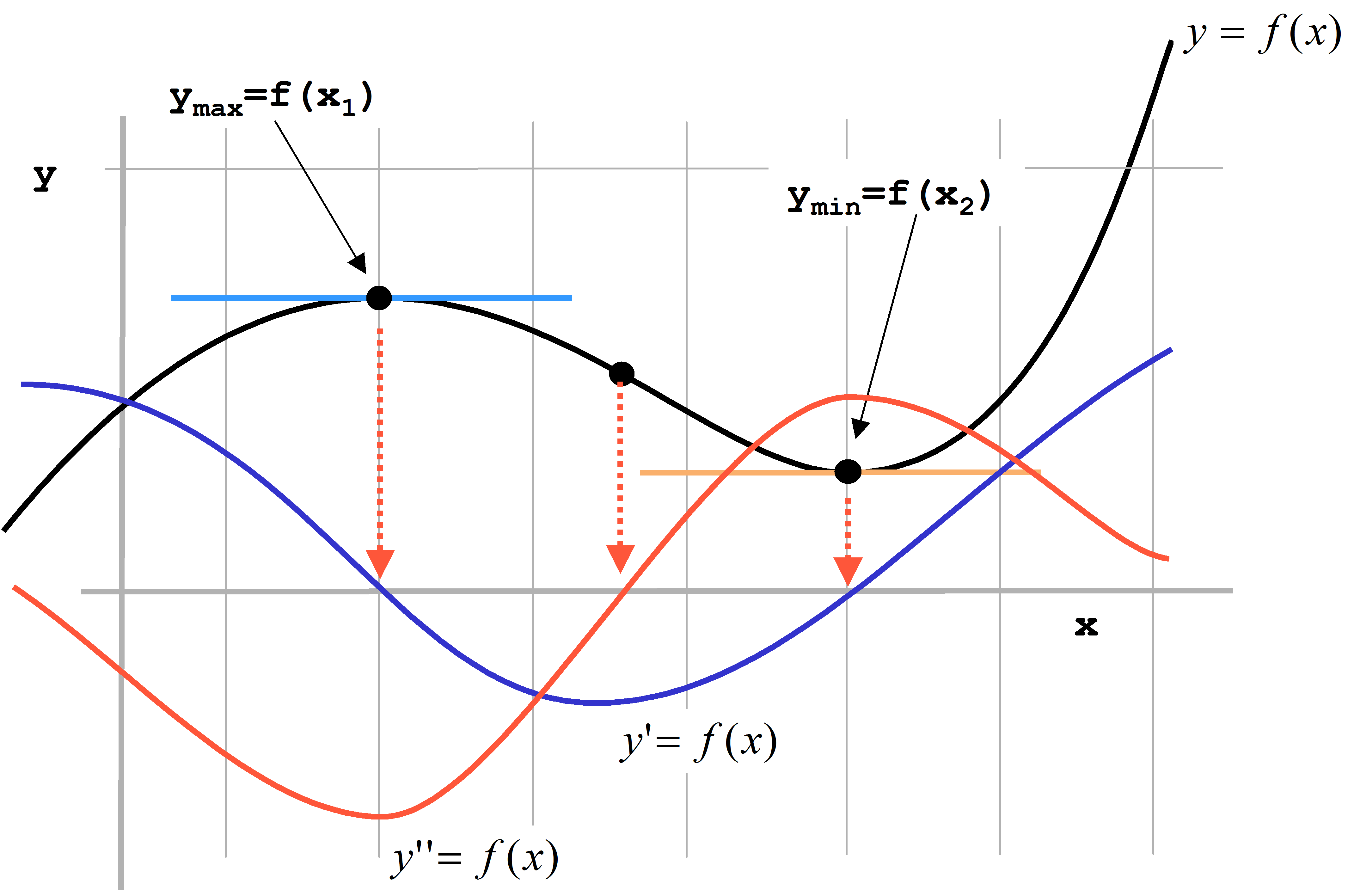
Daraus folgt, dass ein Extremum vorliegt, wenn
\( y' = f'(x) = \frac{ {dy} }{ {dx} } = 0 \quad \Rightarrow \quad \text{ Extremum } \) Gl. 72
Allerdings sagt die Erfüllung dieser Bedingung nichts darüber aus, ob das Extremum ein Minimum oder ein Maximum der Funktion ist. Auskunft darüber gibt die zweite Ableitung der Funktion an den Stellen xextr., an den ein Extremwert gefunden wurde:
\( y'' = f''({x_{extr.} }) = \frac{ { {d^2}y} }{ {d{x^2} } } < 0 \quad \Rightarrow \quad \text{ Maximum } \) Gl. 73
\( y'' = f''({x_{extr.} }) = \frac{ { {d^2}y} }{ {d{x^2} } } > 0 \quad \Rightarrow \quad \text{ Minimum } \) Gl. 74
Darüber hinaus kann auch noch vorhandene Wendepunkte der Funktion gefunden werden:
\( y'' = f''({x_{Wende} }) = \frac{ { {d^2}y} }{ {d{x^2} } } = 0 \\ y''' = f'''({x_{Wende} }) = \frac{ { {d^3}y} }{ {d{x^3} } } \ne 0 \quad \Rightarrow \quad \text{ Wendepunkt } \) Gl. 75
Wendepunkte, die zudem keine Steigung aufweisen (die Tangente im Wendepunkt verläuft parallel zur x-Achse), werden Sattelpunkt genannt. Um einen einfachen Wendepunkt von einem Sattelpunkt zu unterscheiden, wird wieder die erste Ableitung herangezogen:
\( y' = f'({x_{Wende} }) = \frac{ {dy} }{ {dx} }\,\,\,\left\{ { \begin{array}{cc}{ \ne 0 \quad \Rightarrow \quad Wendepunkt} \\ { = 0 \quad \Rightarrow \quad \text{Sattelpunkt} } \end{array} } \right. \) Gl. 76
Beispiel:
Die Dimensionen eines Zylinders sind so zu bestimmen, dass bei vorgegebenem Volumen V0 die Oberfläche O minimal wird.
\( V = h \cdot F = h \cdot \pi \cdot {r^2}; \) Gl. 77
\( O = h \cdot U + 2 \cdot \pi \cdot {r^2} = h \cdot 2 \cdot \pi \cdot r + 2 \cdot \pi \cdot {r^2} \) Gl. 78
Umstellen von Gl. 77 nach der Höhe h ergibt
\( h = \frac{V}{ {\pi \cdot {r^2} } } \) Gl. 79
Einsetzen in Gl. 77
\( O = \frac{ {V \cdot 2 \cdot \pi \cdot r} }{ {\pi \cdot {r^2} } } + 2 \cdot \pi \cdot {r^2} = \frac{ {V \cdot 2} }{ { {r^{} } } } + 2 \cdot \pi \cdot {r^2} \) Gl. 80
Bilden der ersten Ableitung:
\( \frac{ {dO} }{ {dr} } = \frac{ {d\left( {\frac{ {V \cdot 2} }{r} + 2 \cdot \pi \cdot {r^2} } \right)} }{ {dr} } = - \frac{ {V \cdot 2} }{ { {r^2} } } + 4 \cdot \pi \cdot r \) Gl. 81
Null setzen:
\( -\frac{ {V \cdot 2} }{ { {r^2} } } + 4 \cdot \pi \cdot r = 0 \) Gl. 82
Umstellen und nach r auflösen:
\( \frac{V}{ {2 \cdot \pi } } = {r^3} \quad \Rightarrow \quad {r_{extr.} } = \sqrt[3]{ {\frac{V}{ {2 \cdot \pi } } } }\) Extremwert! Gl. 83
Prüfen, ob die Oberfläche O wirklich minimal. D.h. zweite Ableitung bilden. Dazu wird Gl. 81 noch einmal differenziert:
\( \frac{ { {d^2}O} }{ {d{r^2} } } = 2 \cdot \frac{ {V \cdot 2} }{ { {r^3} } } + 4 \cdot \pi \) Gl. 84
\({\left. {\frac{ { {d^2}O} }{ {d{r^2} } } } \right|_{r = {r_{extr.} } } } = 2 \cdot \frac{ {V \cdot 2} }{ {\frac{V}{ {2 \cdot \pi } } } } + 4 \cdot \pi = 12 \cdot \pi > 0 \quad \Rightarrow \quad \text{Minimum!} \) Gl. 85
q.e.d.
