Für integrierbare Funktionen kann in einem vorgegebenen Intervall der mittlere Funktionswert durch Integration bestimmt werden.
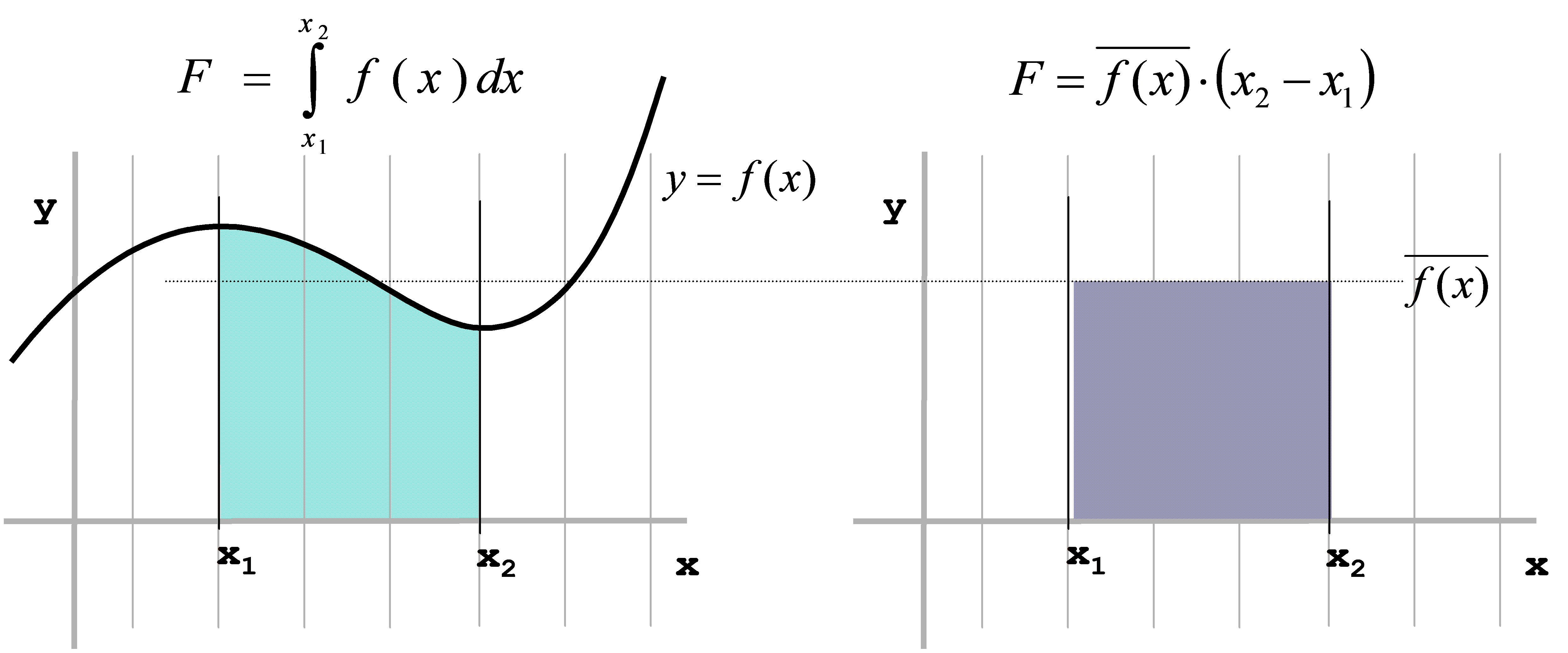
Dazu wird die flächenberechnende Eigenschaft der bestimmter Integrale genutzt, indem eine zu der Integralfläche äquivalente Rechteckfläche im gleichen Intervall berechnet wird. Wird diese Fläche durch die Intervallgröße (Kantenlänge) dividiert, ergibt sich ein mittlerer Funktionswert für dieses Intervall (Abbildung 23). Der mittelwert berechnet sich zu
\( \left. {\overline f \left( x \right)} \right|_{ {x_1} }^{ {x_2} } = \frac{1}{ { {x_2} - {x_1} } }\int\limits_{ {x_1} }^{ {x_2} } {f\left( x \right)dx} \) Gl. 160
