Die Integration bestimmt den Flächeninhalt der Fläche, die zwischen einem von einer Funktion bestimmten Kurvenzug und der x-Achse (unbestimmtes Integral) aufgespannt bzw. zusätzlich durch Anfangs- und Endwerte beschränkt (bestimmtes Integral) wird.
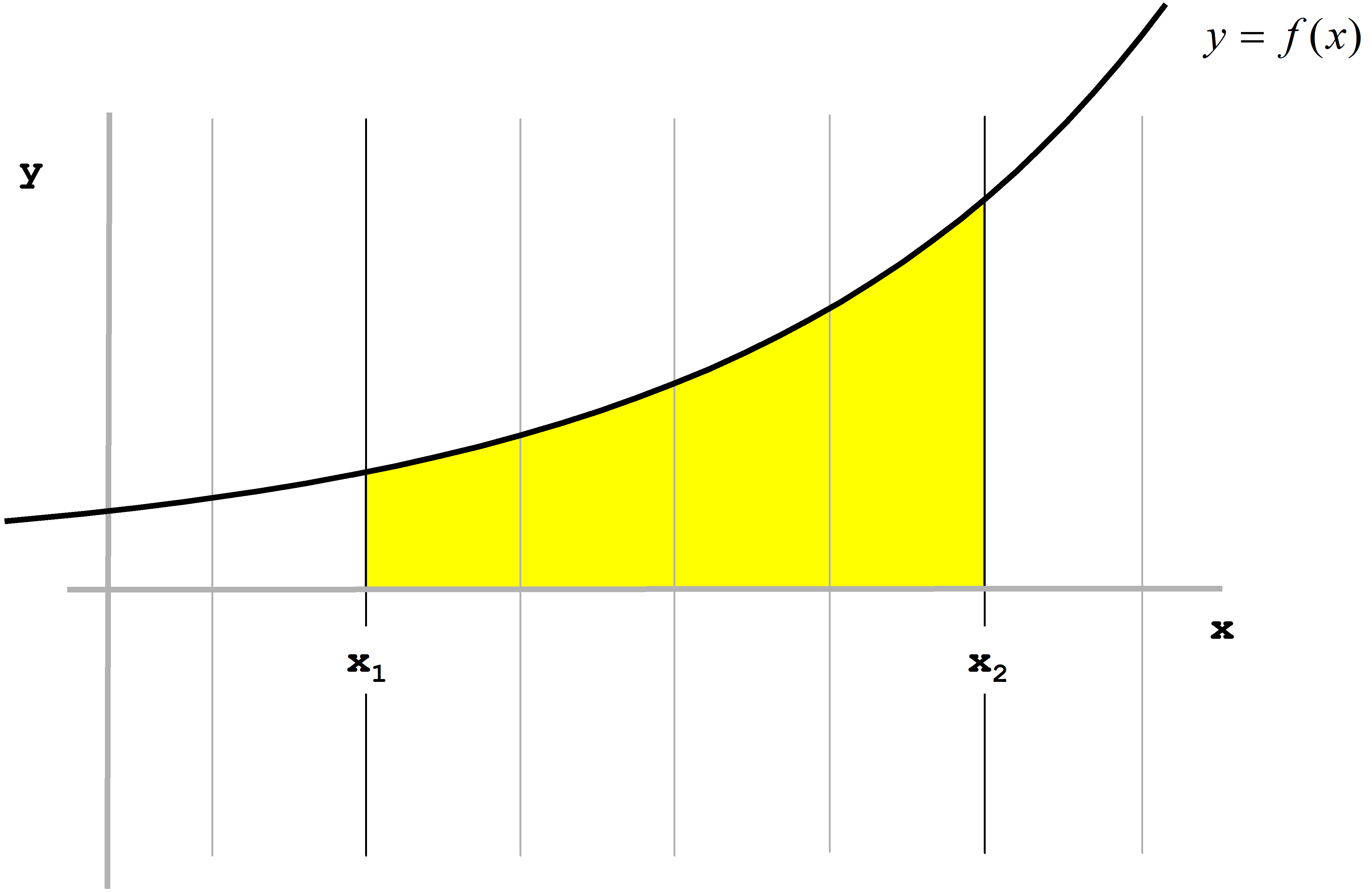
Zur Berechnung der Fläche unter der Kurve wird diese in infinitesimal kleine Streifen der Breite Dx zerlegt. Ihr Flächeninhalt ergibt sich aus dem Produkt von Funktionswert f(x) und Δx (Abbildung 18):
\( \Delta F = f(x) \cdot \Delta x \) Gl. 122
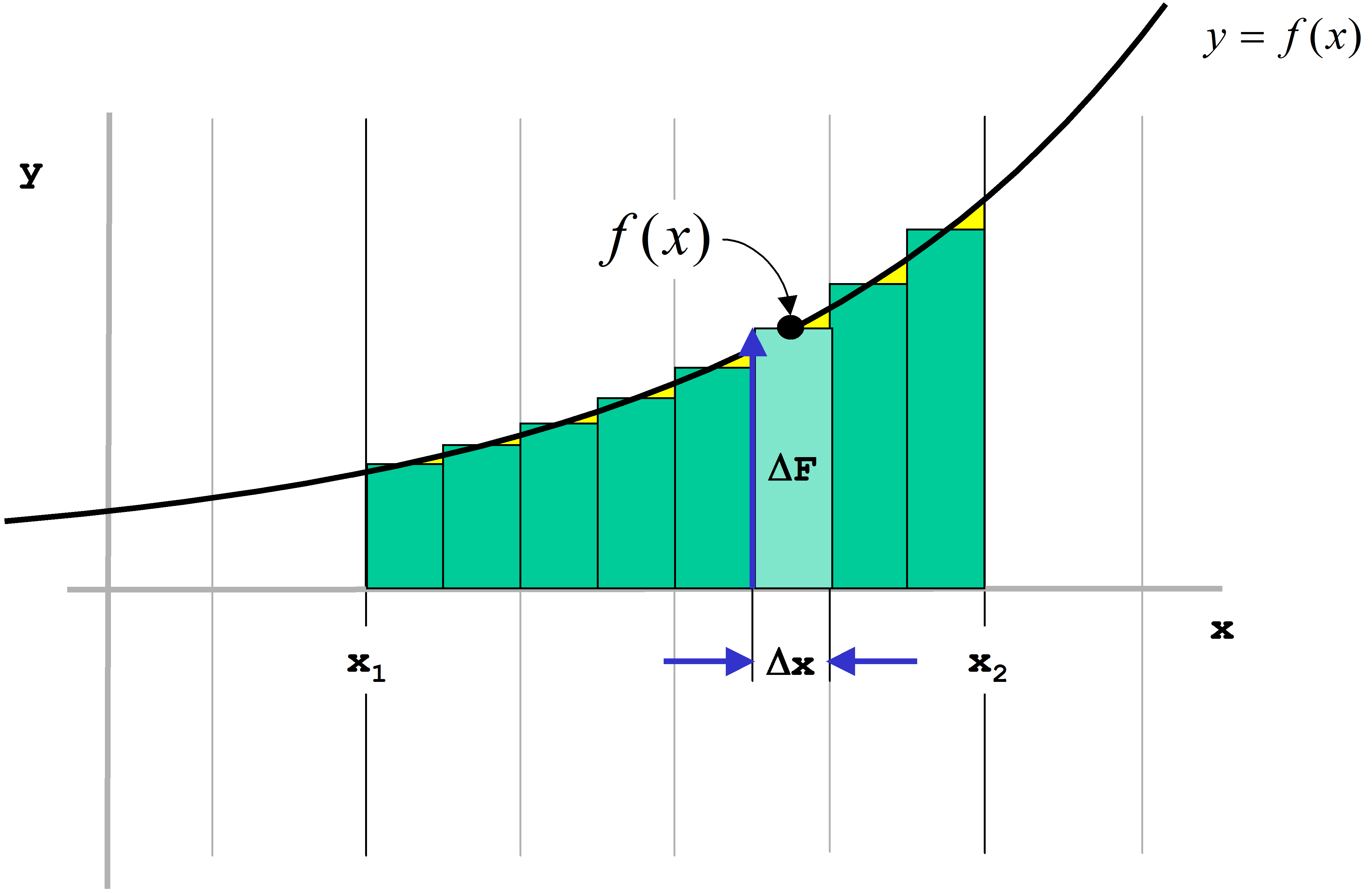
Durch Aufsummation aller Streifen innerhalb eines bestimmten Intervalls wird der Flächeninhalt der gesamten Fläche bestimmt:
\( F = \mathop {\lim }\limits_{\Delta F \to 0} \sum\limits_{ {x_1} }^{ {x_2} } {\Delta F} = \mathop {\lim }\limits_{\Delta x \to 0} \sum\limits_{ {x_1} }^{ {x_2} } {f(x) \cdot \Delta x = \int\limits_{ {x_1} }^{ {x_2} } {f(x) \cdot dx} } \) Gl. 123
Beim Grenzübergang Δx→0 geht das diskrete Summenzeichen \(\sum {} \) in das kontinuierliche Integralzeichen \(\int {} \) über. Die Funktion F(x) heißt Stammfunktion von f(x). Die Funktion f(x) hingegen wird Integrand genannt.
