Das totale Differenzial wir auf Funktionen mit mehreren Variablen angewendet, um die tendenzielle Änderung der Funktion bei Änderung einer oder mehrerer Variablen zu ermitteln.
Wenn das Differenzial einer Funktion von einer Variablen die Steigung einer Tangente in einem bestimmten Punkt repräsentiert, sind dies bei einer Funktion von zwei Variablen zwei Tangenten (Abbildung 16). Nämlich eine bezüglich der z-x-Ebene und eine weitere bezüglich der z-y-Ebene. Beide Tangenten spannen eine Fläche auf, die Funktion in genau diesem Punkt berührt, also die Funktion tangiert.
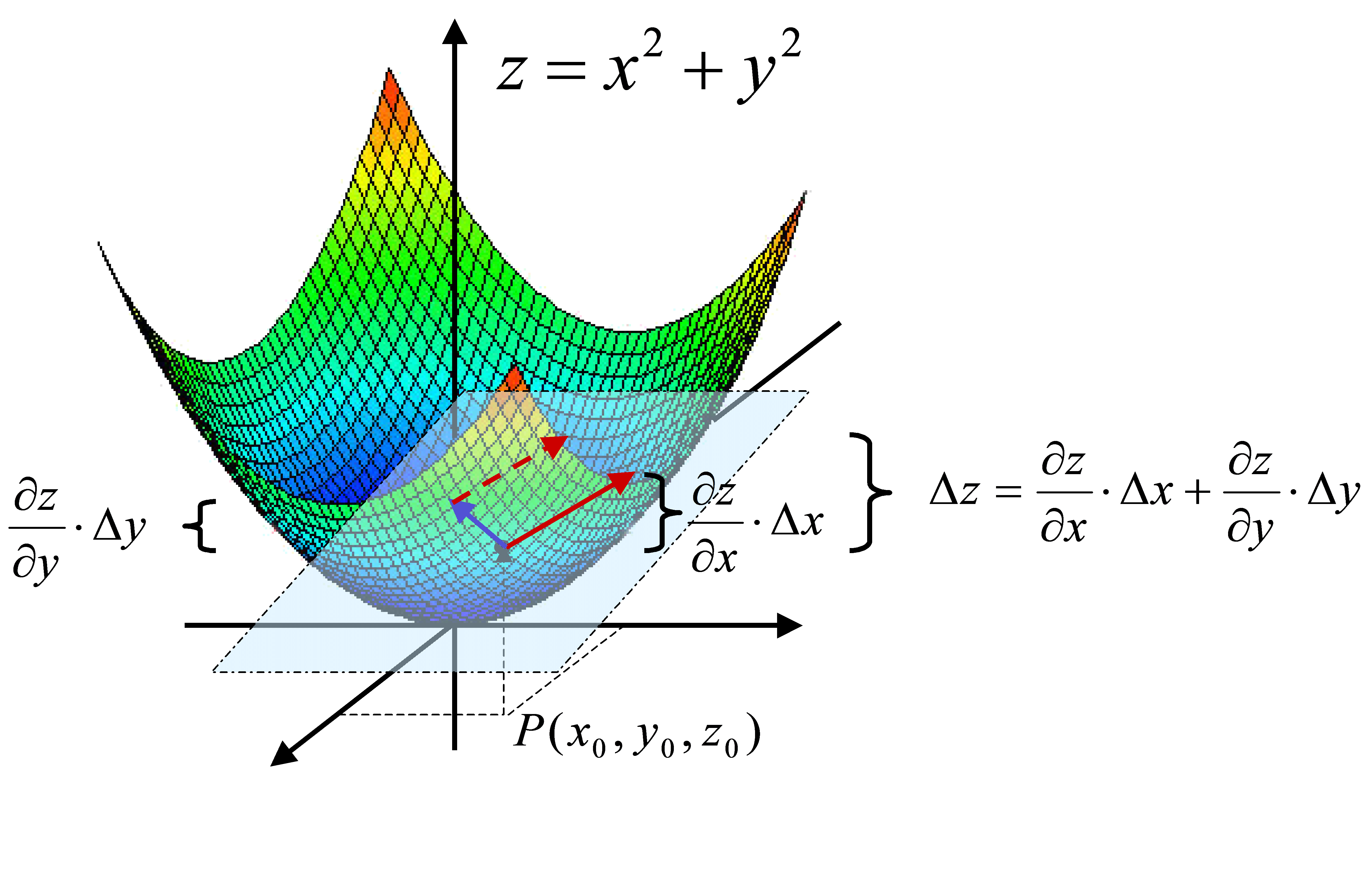
Ausgeführt werden diese Differenziationen dadurch, dass die gesamte Funktion nach der im Nenner bezeichneten Variablen differenziert wird. Alle anderen Variablen werden dabei als Konstanten betrachtet. Sie werden partielle Differenziale der Funktion f(x,y,z) genannt und durch die Symbolik \(\frac{ {\partial f(x,y,z)} }{ {\partial *} }\) ausgedrückt. Dabei verdeutlichen die \(\partial *\), dass es sich bei dieser Differenziation um das partielle Differenzial handelt.
Wie aus Abbildung 16 hervorgeht, ergibt sich die Gesamtänderung dz durch die Summe der Änderungen dx und dy, die von beiden Variablen x bzw. y herrühren:
\( df(x,y,z) = \frac{ {\partial f(x,y,z)} }{ {\partial x} }dx + \frac{ {\partial f(x,y,z)} }{ {\partial y} }dy + \frac{ {\partial f(x,y,z)} }{ {\partial z} }dz \) Gl. 114
Mit Gl. 102 wurde ein Werkzeug zur näherungsweisen Berechnung von Funktionswerten bereit gestellt. Die dazu angestellten Überlegungen werden nun auf Funktionen mit mehreren Veränderlichen angewendet:
\( \tilde f({x_0} + \Delta x,{y_0} + \Delta y,{z_0} + \Delta z) = f({x_0},{y_0},{z_0}) + \frac{ {\partial f(x,y,z)} }{ {\partial x} }\Delta x + \frac{ {\partial f(x,y,z)} }{ {\partial y} }\Delta y + \frac{ {\partial f(x,y,z)} }{ {\partial z} }\Delta z \) Gl. 115
Eine weit verbreitete Anwendung des totalen Differenzials ist die Abschätzung der Auswirkung von Messfehlern auf Messergebnisse (Fehlerfortpflanzung) in komplexen Zusammenhängen:
\( \Delta f = \left| {\frac{ {\partial f(x,y,z)} }{ {\partial x} }\Delta x} \right| + \left| {\frac{ {\partial f(x,y,z)} }{ {\partial y} }\Delta y} \right| + \left| {\frac{ {\partial f(x,y,z)} }{ {\partial z} }\Delta z} \right| \) Gl. 116
Beachte: Zur Fehlerabschätzung werden die jeweiligen Teilbeiträge der einzelnen Variablen in Betragsstriche gesetzt. Damit wird der max. mögliche Fehler abgeschätzt. Die Möglichkeit, dass sich Fehler ggf. auch gegenseitig kompensieren können, wird damit ausgeschlossen.
Beispiel:
In einem Pendelexperiment soll die Größe der Erdbeschleunigung g bestimmt werden, indem die Pendelfrequenz gemessen wird. Dazu wird ein Pendel der Länge L verwendet. Die Länge des Pendels kann mit der Genauigkeit ΔL/L = 0,1 % gemessen werden. Die Periodendauer T der Pendelschwingung wird mit einer Genauigkeit ΔT/T = 2 % gemessen. Wie genau kann damit die Erdbeschleunigung g bestimmt werden?
Die Abhängigkeit der Pendelperiode von der Pendellänge und der Erdbeschleunigung ist gegeben durch:
\( T = \frac{1}{ {2\pi } }\sqrt {\frac{L}{g} } \) Gl. 117
umstellen nach g
\( g = \frac{1}{ {4{\pi ^2} } }\frac{L}{ { {T^2} } } \) Gl. 118
Bildung der partiellen Ableitungen und daraus des totalen Differenzials:
\( \Delta g = \frac{1}{ {4{\pi ^2} } }\left[ {\left| {\frac{1}{ { {T^2} } } \cdot \Delta L} \right| + \left| { - 2 \cdot \frac{L}{ { {T^3} } } \cdot \Delta T} \right|} \right] \) Gl. 119
Erweitern mit 1/g:
\( \frac{ {\Delta g} }{g} = \frac{1}{ {4{\pi^2} } }\left[ {\left| {\frac{1}{ { {T^2} } } \cdot \Delta L} \right| + \left| { - 2 \cdot \frac{L}{ { {T^3} } } \cdot \Delta T} \right|} \right]\frac{1}{g} \) Gl. 120
mit Gl. 118 und sortieren
\( \left| {\frac{ {\Delta g} }{g} } \right| = \left| {\frac{ {\Delta L} }{L} } \right| + \left| {\frac{ {2\Delta T} }{T} } \right| = 0,1\% + 4\% = 4,1\% \) Gl. 121
zeigt, dass die Messfehler beider Variablen gleichberechtigt in das Resultat eingehen, das mit einer Genauigkeit von 4,1 % bestimmt werden kann. Es ist aber auch zu ersehen, dass Messfehler der Zeitmessung stärker eingehen als die der Längenmessung.
