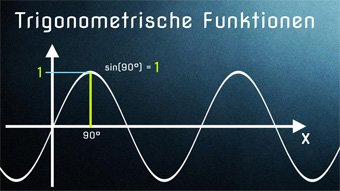
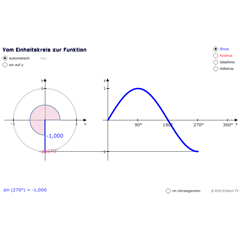
Erinnern wir uns an die Zuordnung im Einheitskreis:
Ein Winkel α (an der Kreislinie abzulesen) erhält einen Sinuswert (die Höhe, siehe y-Achse). Den x-Wert ignorieren wir (dies wäre der Kosinuswert des Winkels).
0° hat die Höhe 0 → sin(0°) = 0
60° hat die Höhe ca. 0,866 → sin(60°) ≈ 0,866
allgemein: Winkel 0 hat die Höhe y → sin(α) = y
Tragen wir diese Wertepaare Winkel und Sinuswert (allgemein als Punkt (α|sin(α))) in ein zweites Koordinatensystem ein. Am Einheitskreis lesen wir hierzu auf der Kreislinie die Winkel von 0° bis 360° ab, und die Höhe y zeigt uns die Sinuswerte an.
In dem zweiten Koordinatensystem tragen wir die Winkel auf der x-Achse ein. Also 0°, 90°, 180°, 270° und 360°. Stellen wir uns vor, dass wir die Kreislinie aufschneiden und abrollen.
Aber aufpassen: Die x-Werte im zweiten Koordinatensystem sind die Winkelwerte in Grad. Im Gegensatz dazu ist das x am Einheitskreis der Kosinuswert, den wir uns später anschauen.
Setzen wir für jeden einzelnen Winkel die entsprechende Höhe (den Sinuswert) ein. Jeder Winkel bekommt eine Höhe (Sinuswert) zugeordnet.
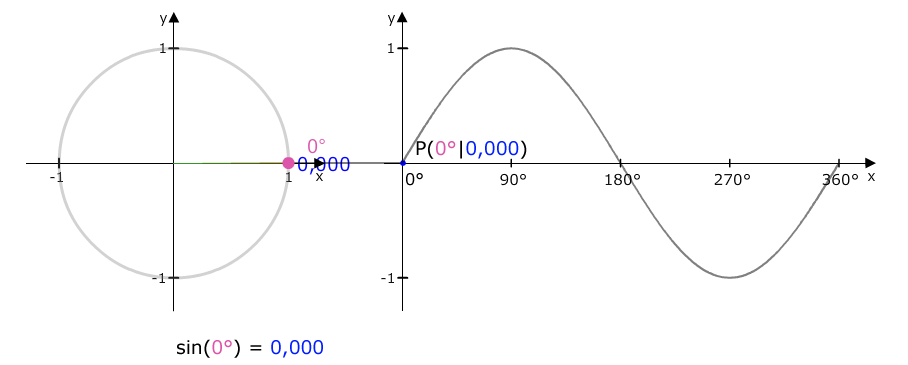
Bei 0° haben wir eine Höhe von 0, siehe y-Achse, der y-Wert ist 0 (das ist unser Sinuswert). Wir merken uns sin(0°) = 0.
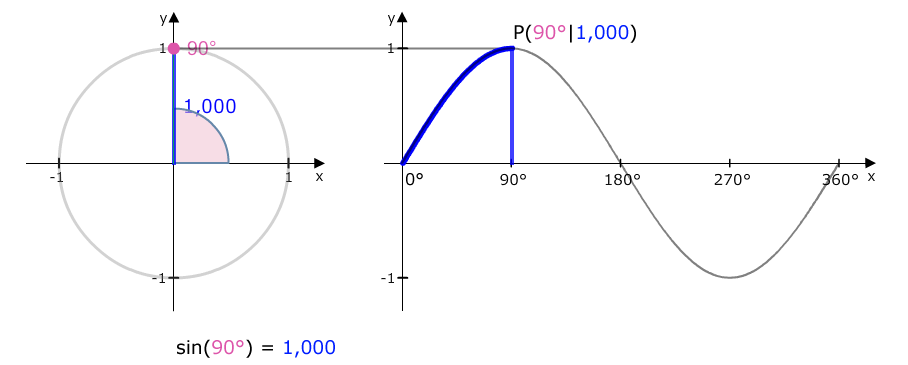
Wir erkennen, dass sich bei den Winkelwerten von 0° bis 90° die Sinuswerte von 0 auf 1 erhöhen. Bei 90° erreichen wir schließlich die 1, der maximale Wert, den Sinus annehmen kann.
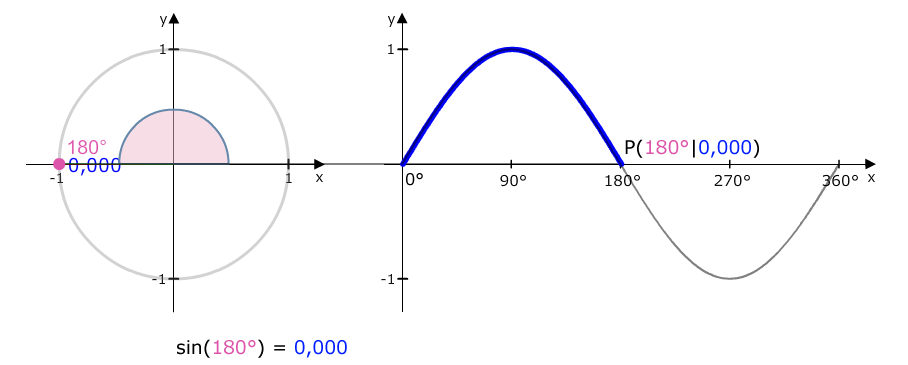
Von 90° bis 180° nimmt der Sinuswert wieder ab und bewegt sich Richtung 0. Bei 180° erreicht er 0.
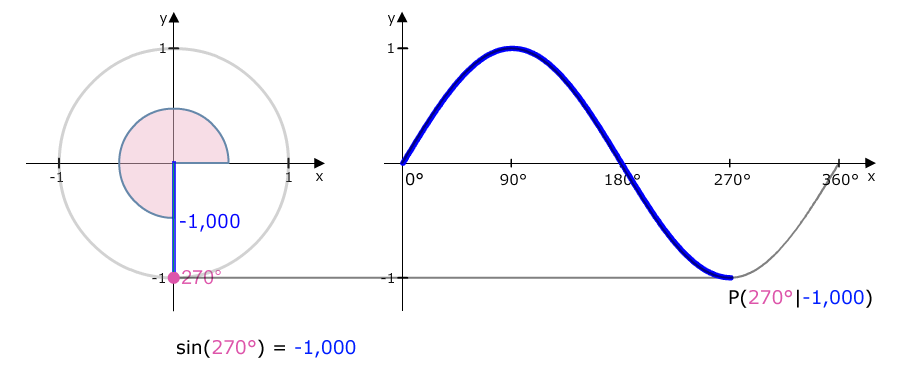
Von 180° bis 270° werden die Sinuswerte negativ, weil wir uns unterhalb von y = 0 befinden. Wenn wir 270° erreichen, dann haben wir den Sinuswert -1. Also: sin(270°) = -1.
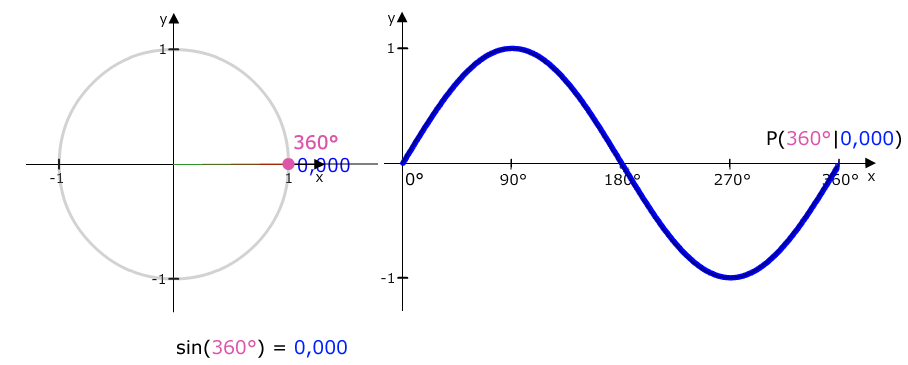
Gehen wir von 270° zu 360° nimmt unser Sinuswert von -1 bis 0 wieder zu. Bei 360° ist der Sinuswert 0.
Wie wir sehen, ergibt sich auf diese Weise der Graph der Sinusfunktion von 0° bis 360°. Hier können wir für jeden Winkel (x-Achse) den entsprechenden Sinuswert (y-Achse) ablesen.
Dieser Funktionsgraph wird wegen seines Verlaufs auch auch „Sinuskurve“ oder „Sinusschwingung“ genannt.
Entstehung des Sinusgraphen (Animation)
Schauen wir uns das als Animation an. Wir laufen den Einheitskreis entlang und zeichnen Winkel und Sinuswert (Höhe) in das zweite Koordinatensystem ein.
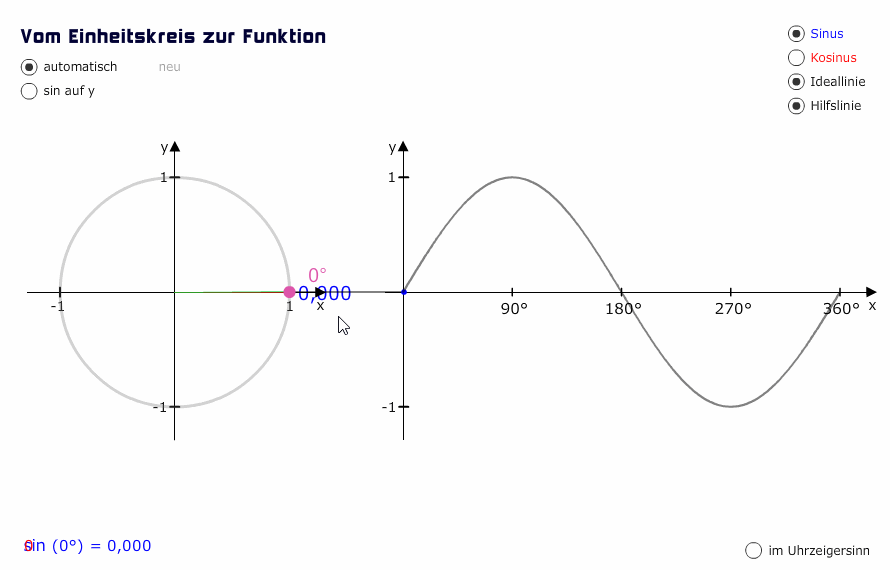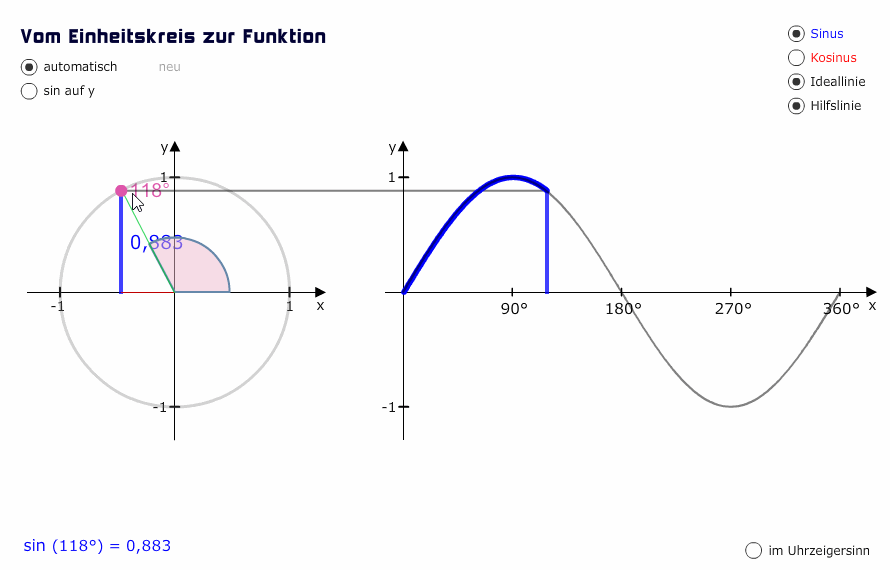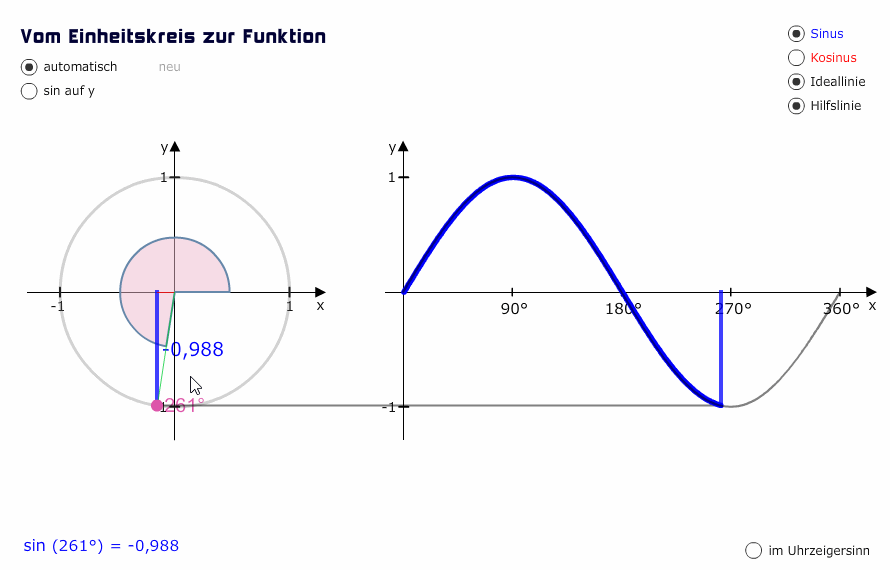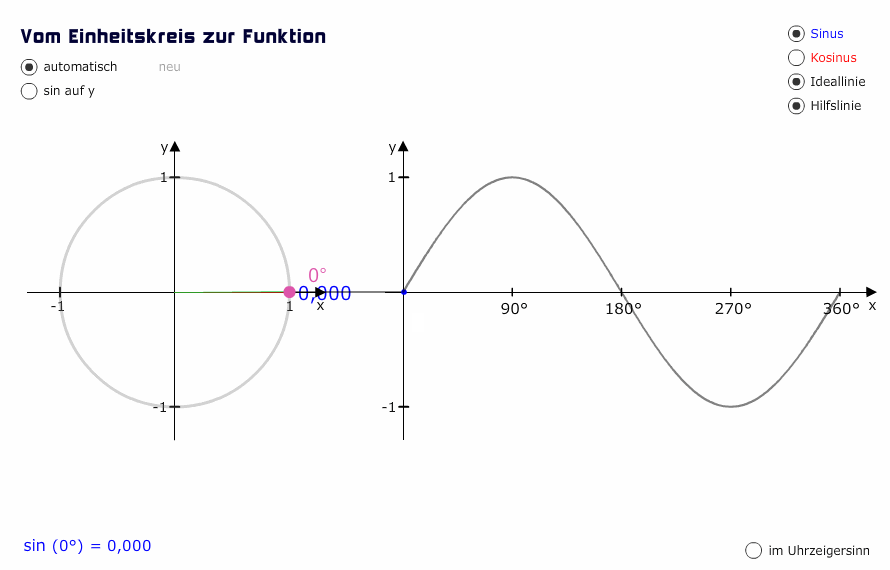
Um Sinuswerte zu ermitteln, können wir jetzt statt des Einheitskreises die Sinusfunktion benutzen. Wenn uns also jemand nach sin(90°) fragt, können wir mit Blick auf den Graphen erkennen, dass bei 90° der Sinuswert 1 ist.
Bei sin(180°) ist der Sinuswert 0. Bei sin(270°) beträgt er -1 und bei 360° haben wir den Sinuswert 0.
Jetzt kennen wir den Zusammenhang zwischen Einheitskreis und Sinusfunktion.