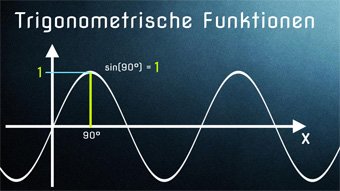
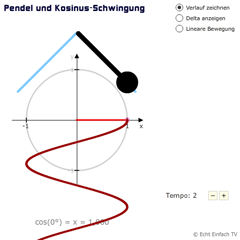
Eine Kosinusschwingung können wir mit einem Pendel erzeugen.
Wenn wir ein Pendel loslassen, wird es von links nach rechts schwingen. Es hat links bzw. rechts den maximalen Ausschlag mit einer Geschwindigkeit von 0. In der Mitte ist es am schnellsten.
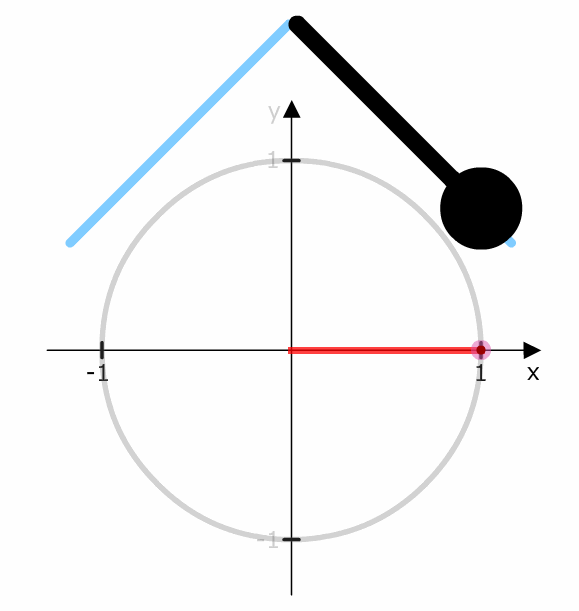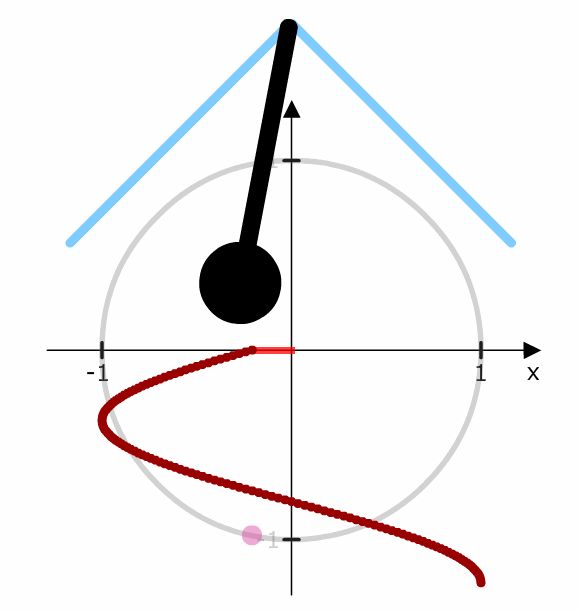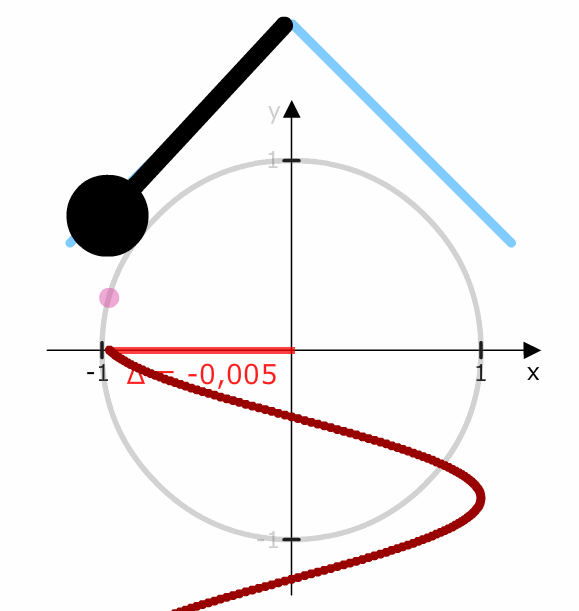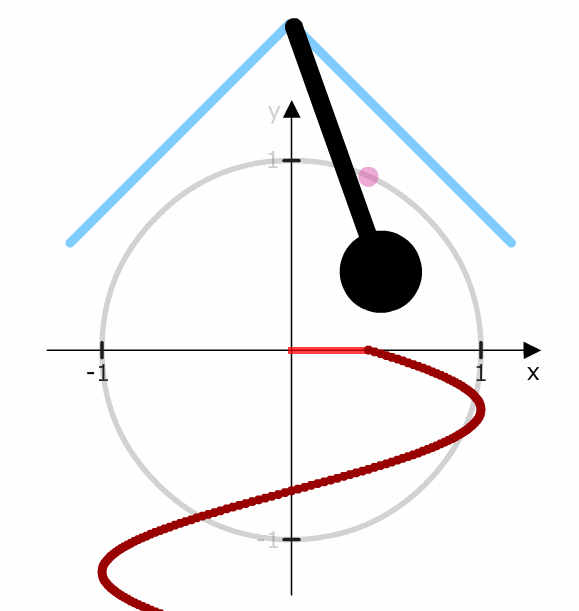
Schauen wir uns zum Vergleich eine lineare Bewegung an. In diesem Fall bewegt sich das Pendel mit gleichen Schritten nach links bzw. rechts.
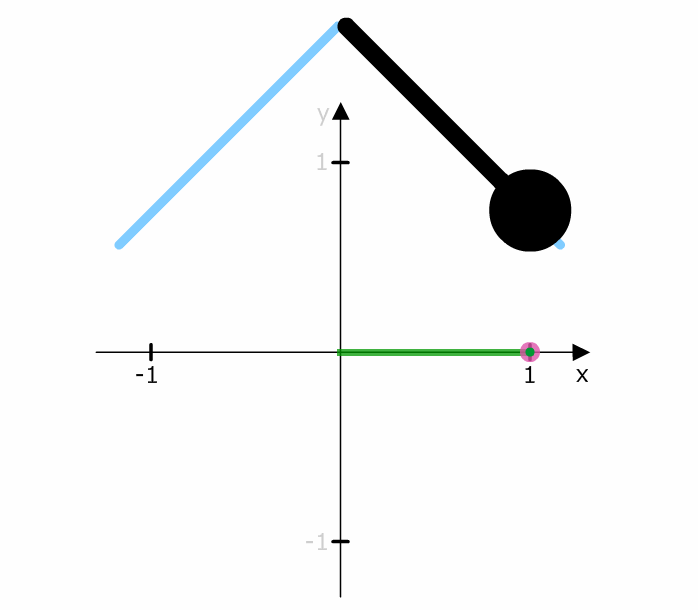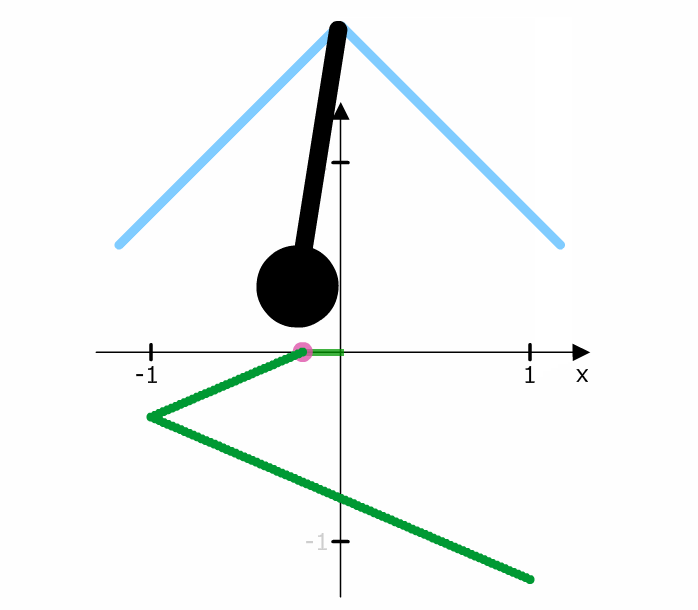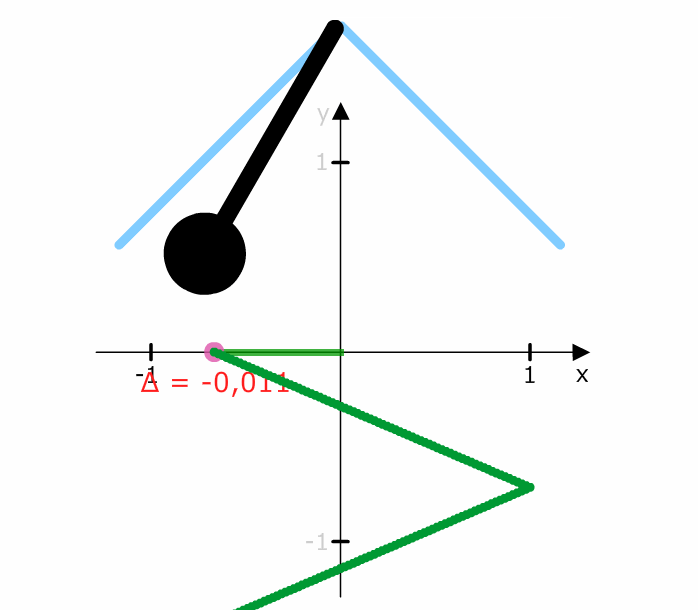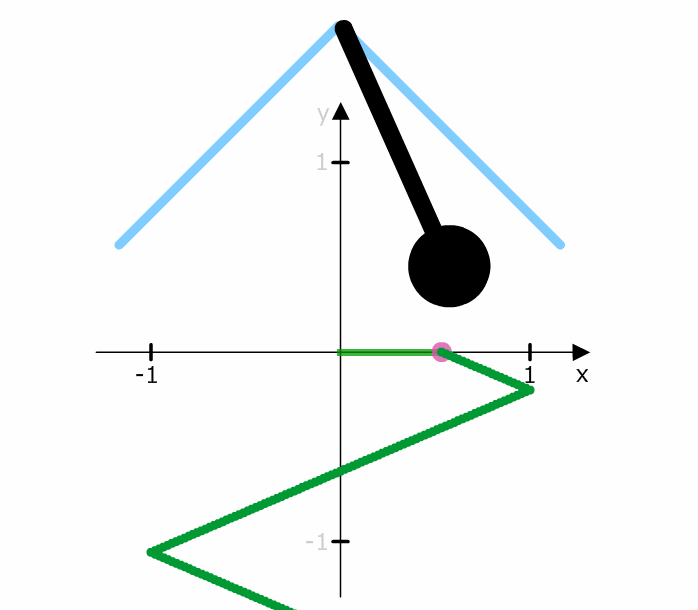
Die Schritte bei der linearen Bewegung sind immer konstant.
Die Schritte bei der Kosinusschwingung sind unterschiedlich.
Hier ein paar Beispiel für solche unterschiedlichen Kosinuswerte:
cos(1°) ≈ 1,000 und cos(1°+1°) = cos(2°) = 0,999 ergibt Differenz 0,001.
cos(24°) = 0,914 und cos(24°+1°) = cos(25°) = 0,906 ergibt Differenz 0,008.
cos(45°) = 0,707 und cos(45°+1°) = cos(46°) = 0,695 ergibt Differenz 0,012.
Gehen wir einen „Winkelschritt“ von 1° zu 2° legen wir nur 0,001 zurück. Gehen wir einen „Winkelschritt“ von 24° zu 45° legen wir 0,008 zurück, also nicht den gleichen Wert, sondern einen veränderten (höheren) Wert.