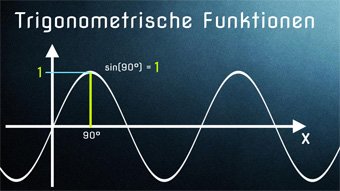
Wenn wir das Gleiche (siehe Graph der Sinusfunktion im Einheitskreis) mit dem Kosinusgraphen machen möchten, müssen wir ihn von oben nach unten zeichnen.
Auch hier erkennen wir die periodische Schwingung:
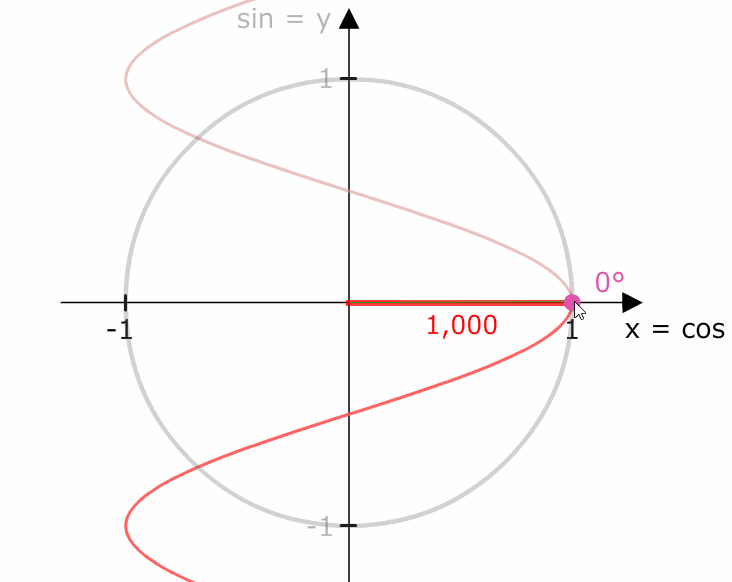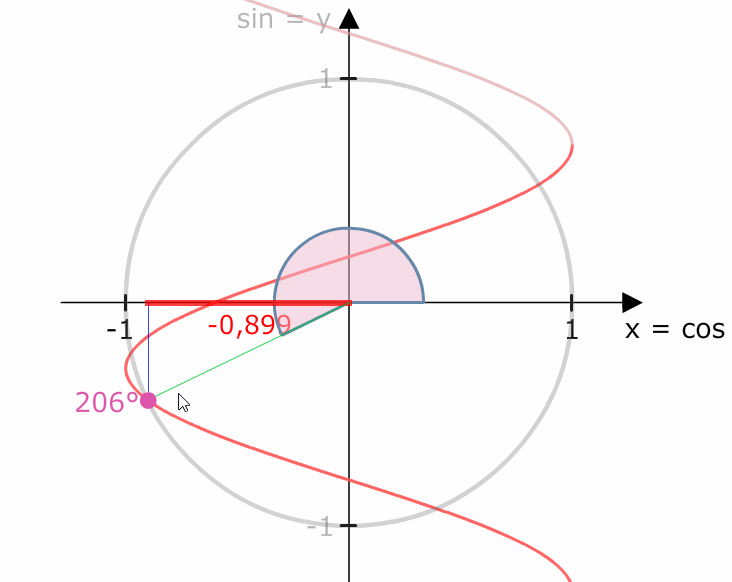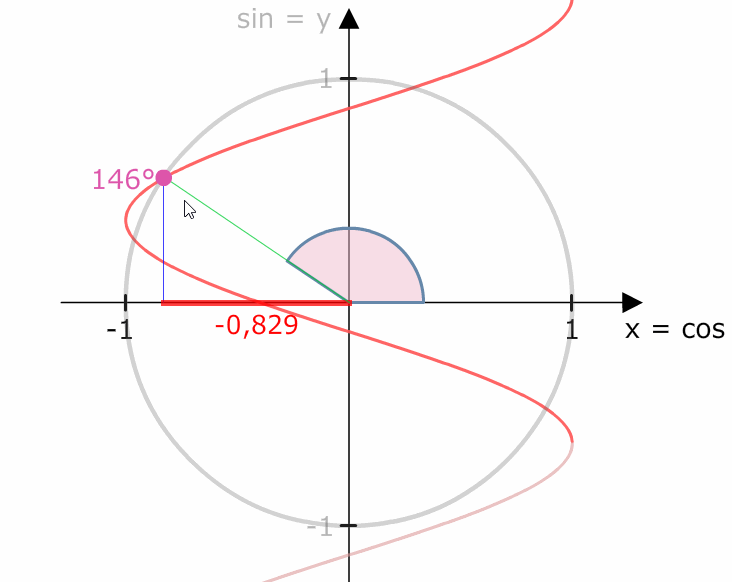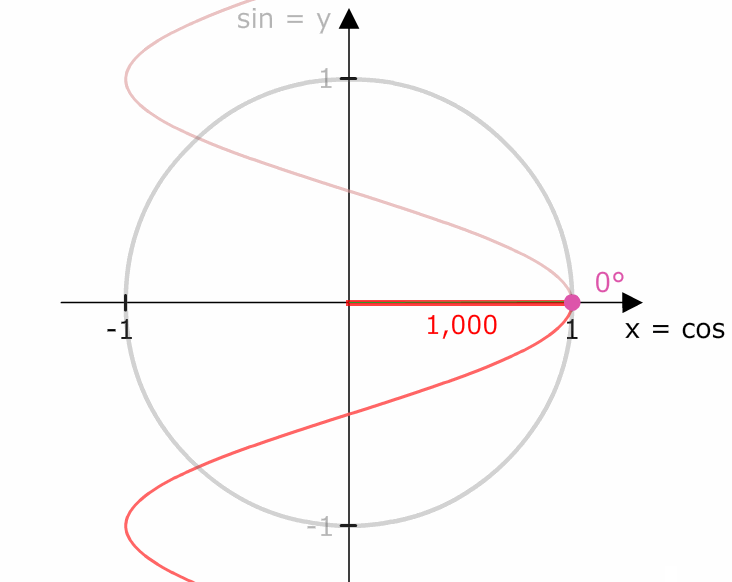
Der Kosinusgraph ist periodisch, denn all seine Werte wiederholen sich jede 360°.