Die Multiplikation ist eine verkürzte Schreibweise der Addition. Anstatt 4 + 4 + 4 zu schreiben, zählen wir die Anzahl der Vieren (hier sind es 3) und schreiben stattdessen: 3 · 4 ("drei mal vier"). Es sind 3 Vieren, die miteinander addiert werden sollen.

Eine Zahl (Faktor) wird mit einer anderen Zahl (Faktor) multipliziert und das Ergebnis nennt man Produkt.
Das Zeichen der Multiplikation ist meist ein Punkt ·. Als Multiplikationszeichen („Malzeichen“) kann jedoch auch ein kleines Kreuz gesetzt werden 3×5.
Multiplikationstabelle
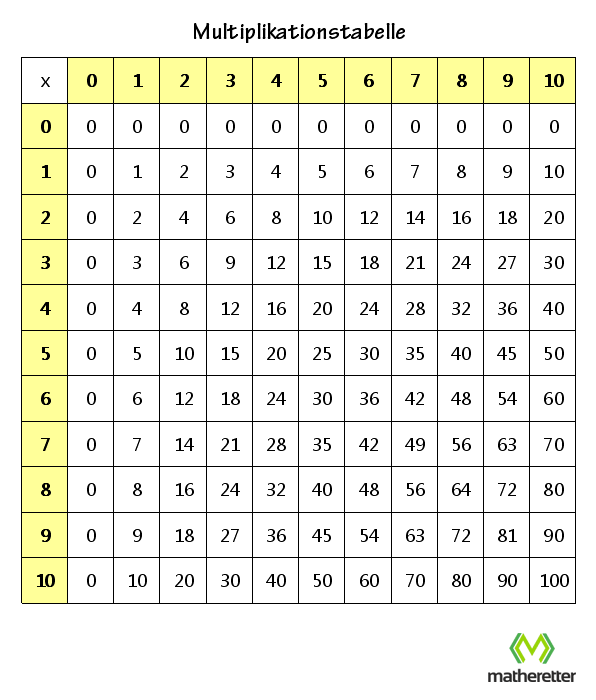
Kopfrechnen gut zu beherrschen ist sehr wichtig für den Mathematik-Unterricht aber auch den Alltag, zum Beispiel beim Einkaufen. Daher könnt ihr die folgende Multiplikationstabelle (auch „kleines Einmaleins“ genannt) als Hilfsmittel benutzen. Druckt sie einfach aus und übt mit ihr die Multiplikationen (trainiert die Zahlen von 0 mal 0 bis 10 mal 10), falls ihr noch nicht sicher seid:
Allgemein benennt man:
9 · 6 = 36
Faktor · Faktor = Produkt
Multiplikationstabelle
Download Als Excel-Datei Als PDF-Datei
Auch gibt es bei den Lernprogrammen ein zweites Programm, mit dem ihr die Grundrechenarten mit verschiedenen Zahlen testen könnt (Berechnung erfolgt automatisch).
Abschließend der Hinweis: Das neutrale Element der Multiplikation ist die Eins, denn durch diese ändert sich der Wert nicht. Zum Beispiel: 8 · 1 = 8
Rechentipp zur Multiplikation
Sich das richtige Ergebnis einiger Multiplikationen zu merken, scheint manchmal schwierig. Ein gutes Beispiel ist: 6·7 ... kommt 42 oder 43 heraus? Hierzu merkt euch den Rechentipp, dass die Multiplikation einfach zerlegt werden kann:
6·7 = (3+3)·7 = 3·7 + 3·7 = 21 + 21 = 42
Anders gesagt: Wenn wir wissen, dass 3·7 = 21 ist, dann kann 6·7 nur das Doppelte von 21 also 42 sein.
43 ist übrigens eine Primzahl, kann also per Multiplikation nur mit 1·43 gebildet werden. ;-)
Multiplikationszeichen am Computer
Neben den Multiplikationszeichen · und × kann man am Computer direkt den Stern * verwenden. Dieser befindet sich auf dem Nummernblock der Tastatur rechts, man schreibt dann zum Beispiel 3*5.
Weiterhin kann man neben dem kleinen Punkt · auch einen dicken Punkt • verwenden. Um dies am Computer einzugeben, muss man auf der Tastatur ALT gedrückt halten und auf dem Nummernblock drücken: ALT+0183 ergibt · und ALT+7 ergibt •

