Lektion F07: Quadratische Funktionen / Parabeln
Nachdem wir nun die linearen Funktionen vollständig verstanden haben, können wir uns als nächstes die quadratischen Funktionen betrachten.
Quadratische Funktionen - Einführung Parabel
Einführung zur Quadratischen Funktion über die Fläche eines Quadrats, Hinleitung zur Normalparabel, Streckung und Stauchung einer Parabel
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
F07-2 Quadratische Funktionen - Parabel und ScheitelpunktScheitelpunkt und Scheitelpunktform, Verschiebung der Parabel, Auswirkung von Streckung und Stauchung auf die Gleichung der Funktion
-
F07-3 Quadratische Funktionen - Quadratische ErgänzungScheitelpunkt bestimmen, Scheitelpunktform und Allgemeinform, Erklärung der Quadratischen Ergänzung unter Anwendung der Binomischen Formeln.
-
F07-4 Quadratische Funktionen - Nullstellen bei ScheitelpunktformQuadratische Ergänzung bei einem Faktor vor x², Ermittlung von Nullstellen bei der Scheitelpunktform
-
F07-5 Quadratische Funktionen - p-q-Formel und Nullstellenp-q-Formel zur Ermittlung der Nullstellen einer Quadratischen Funktion, Anwendung und Herleitung
-
F07-6 Quadratische Funktionen - DiskriminanteBegriff Diskriminante, Lösungsmöglichkeiten bei der Diskriminante (p-q-Formel).
-
F07-7 Quadratische Funktionen - Satz von VietaHerleitung für den Satz von Vieta. Anwendungsbeispiele.
-
F07-8 Quadratische Funktionen - LinearfaktorenLinearfaktoren bei der Quadratischen Funktion, Funktionsgleichung aufstellen über Nullstellen und Linearfaktoren
-
F07-9 Funktionsplotter + ZusammenfassungIn diesem Video erklären wir anhand eines Programms zum Zeichnen von Funktionen, wie sich die einzelnen Funktionen (0. bis 3. Grad) ergeben.
-
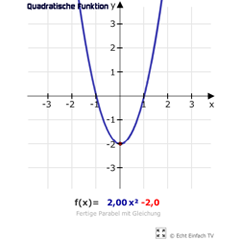 Parabel der Form a·x²+n erstellenVerschiebt die Parabel entlang der y-Achse (mit Mausklick bestätigen) und stellt danach ihre Steigung ein.
Parabel der Form a·x²+n erstellenVerschiebt die Parabel entlang der y-Achse (mit Mausklick bestätigen) und stellt danach ihre Steigung ein. -
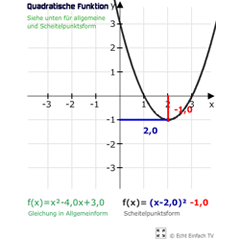 Scheitelpunkt- und AllgemeinformVerschiebt die Parabel und seht dabei ihre Gleichung in Scheitelpunktform f(x)=(x-v)²+n. Ein Klick mit der Maus verrät euch dann die Allgemeinform f(x)=x²+bx+c.
Scheitelpunkt- und AllgemeinformVerschiebt die Parabel und seht dabei ihre Gleichung in Scheitelpunktform f(x)=(x-v)²+n. Ein Klick mit der Maus verrät euch dann die Allgemeinform f(x)=x²+bx+c. -
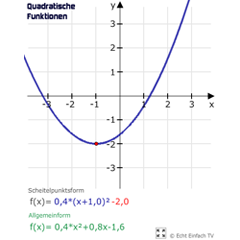 Parabel mit Streckung/StauchungHier erkennt ihr den Zusammenhang zwischen Scheitelpunktform mit f(x)=a·(x-v)²+n und Allgemeinform f(x)=ax²+bx+c bei beliebigem Scheitelpunkt und beliebiger Streckung/Stauchung.
Parabel mit Streckung/StauchungHier erkennt ihr den Zusammenhang zwischen Scheitelpunktform mit f(x)=a·(x-v)²+n und Allgemeinform f(x)=ax²+bx+c bei beliebigem Scheitelpunkt und beliebiger Streckung/Stauchung. -
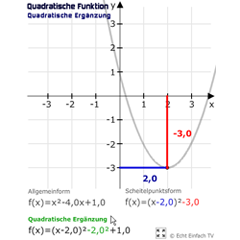 Quadratische ErgänzungBeim Verschieben der Parabel wird live die Quadratische Ergänzung berechnet. Die Allgemeinform lässt sich mit Hilfe der Quadratischen Ergänzung in die Scheitelpunktform zurückführen.
Quadratische ErgänzungBeim Verschieben der Parabel wird live die Quadratische Ergänzung berechnet. Die Allgemeinform lässt sich mit Hilfe der Quadratischen Ergänzung in die Scheitelpunktform zurückführen. -
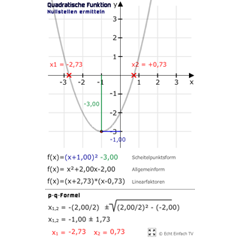 Nullstellen der Parabel finden (p-q-Formel)Hier könnt ihr die Nullstellen einer Parabel mittels p-q-Formel ermitteln. Versetzt die Parabel mit der Maus und seht live die sich ergebenden Nullstellen!
Nullstellen der Parabel finden (p-q-Formel)Hier könnt ihr die Nullstellen einer Parabel mittels p-q-Formel ermitteln. Versetzt die Parabel mit der Maus und seht live die sich ergebenden Nullstellen! -
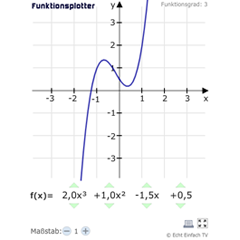 Funktionsplotter (bis 3. Grad)Mit diesem Programm könnt ihr beliebige Funktionen interaktiv zeichnen. Funktionen vom 0. bis 3. Grad sind möglich. Der Funktionsgrad ergibt sich aus der höchsten Potenz.
Funktionsplotter (bis 3. Grad)Mit diesem Programm könnt ihr beliebige Funktionen interaktiv zeichnen. Funktionen vom 0. bis 3. Grad sind möglich. Der Funktionsgrad ergibt sich aus der höchsten Potenz.
Hier findest du 8 Arbeitsblätter, mit denen du dein Wissen testen kannst.
-
AB: Lektion Quadratische Funktionen (Teil 1)
-
AB: Lektion Quadratische Funktionen (Teil 2)
-
AB: Lektion Quadratische Funktionen (Teil 3)
-
AB: Lektion Quadratische Funktionen (Teil 4)
-
AB: Lektion Quadratische Funktionen (Teil 5)
-
AB: Lektion Quadratische Funktionen (Teil 6)
-
AB: Lektion Quadratische Funktionen (Teil 7)
-
AB: Lektion Quadratische Funktionen (Teil 8)
Hier findest du 4 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Quadratische Funktionen - Formelübersicht ❤️
- Quadratische Funktionen - Einführung
- Normalparabel
- Verschobene Normalparabel
- Normalparabel mit Stauchung und Streckung
- Allgemeinform einer quadratischen Funktion
- Normalform einer quadratischen Funktion
- Scheitelpunkt und Scheitelpunktform
- Quadratische Ergänzung
- Nullstellen der Parabel mit Scheitelpunktform bestimmen
- Nullstellen mit Hilfe der p-q-Formel
- Nullstellen mit Hilfe der abc-Formel
- Nullstellen bei f(x) = ax² - c (kein lineares Glied)
- Nullstellen bei f(x) = ax² + bx (kein konstantes Glied)
- Linearfaktoren / Linearfaktorform
- Diskriminante
- Satz von Vieta
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.