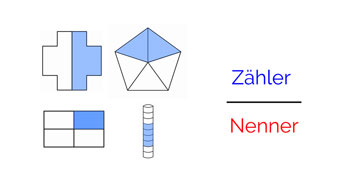
Wir hatten gelernt, wie wir Brüche als Anteile verstehen und aus Zeichnungen den Anteil (also den Wert für Zähler und Nenner) ablesen können. Im Folgenden betrachten wir kurz, wie wir aus einem Bruch eine Zeichnung erstellen können.
Bruch (1/4) am Kreis zeichnen
Unser Bruch lautet: \( \large{\frac{ \textcolor{#00F}{1} }{ \textcolor{#F00}{4}} } \)
Wir wissen, dass der Kreis in 4 Stücke zerlegt werden muss. 1 beliebiges Stück ist dabei auszuwählen bzw. zu färben.
Wir zeichnen also einen Kreis und teilen ihn in 4 gleich große Stücke. Den 360° Vollkreis teilen wir durch 4, also 360°:4 = 90° je Kreissegment. Dann färben wir ein beliebiges Stück farbig.
Wir sprechen „1 von 4“ bzw. „ein Viertel“.
Bruch (3/8) am Kreis zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{3}}{\textcolor{#F00}{8}}} \)
Wir wissen, dass der Kreis in 8 Stücke zerlegt werden muss. 3 beliebige Stücke sind zu färben.
Wir zeichnen also einen Kreis und teilen ihn in 8 gleich große Stücke. Den 360° Vollkreis teilen wir durch 8, also 360°:8 = 45° je Kreissegment. Dann färben wir 3 beliebige Stücke blau. Sie müssen nicht nebeneinander liegen!
Wir sprechen „3 von 8“ bzw. „drei Achtel“.
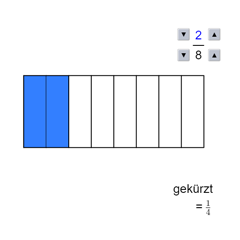
Bruch (2/4) am Rechteck zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{2}}{\textcolor{#F00}{4}}} \)
Wir wissen, dass das Rechteck in 4 gleich große Stücke zerlegt werden muss. 2 beliebige Stücke sind zu färben.
Wir zeichnen also ein Rechteck und teilen es in 4 gleich große Stücke. Dazu halbieren wir Länge und Breite und zeichnen die Striche entsprechend ein. Es entstehen 4 gleich große Stücke. Dann färben wir 2 beliebige Stücke blau.
Wir sprechen „2 von 4“ bzw. „zwei Viertel“.
Bemerkung: \( \frac{2}{4} \) entspricht „1 von 2“ und ist als gekürzter Bruch damit \( \frac{1}{2} \).
Bruch (2/7) am Streifen zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{2}}{\textcolor{#F00}{7}}} \)
Wir wissen, dass der Streifen in 7 gleich große Stücke zerlegt werden muss. 2 beliebige Stücke sind zu färben.
Wir zeichnen also ein Rechteck (unseren Streifen) und teilen es in 7 gleich große Stücke. Dazu rechnen wir die Seitenlänge (z. B. 10 cm) durch 7 (10 cm : 7 ≈ 1,43 cm), diesen Abstand tragen wir nun schrittweise ab und zeichnen die Striche entsprechend senkrecht ein. Es entstehen 7 gleich große Stücke. Dann färben wir 2 beliebige Stücke blau.
Wir sprechen „2 von 7“ bzw. „zwei Siebentel“ (oder „zwei Siebtel“).
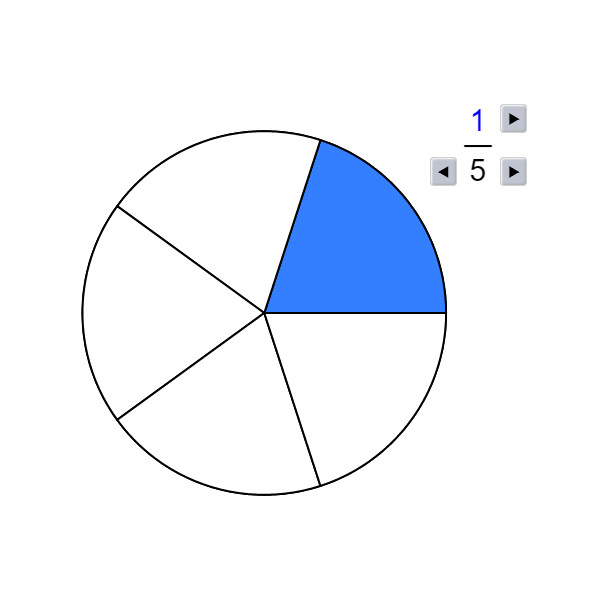
Bruch (2/5) am Fünfeck zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{2}}{\textcolor{#F00}{5}}} \)
Wir wissen, dass das Fünfeck in 5 gleich große Dreiecke zerlegt werden kann. Hierzu sind die Eckpunkte einfach mit dem Mittelpunkt zu verbinden. Danach färben wir 2 beliebige Stücke ein.
Wir sprechen „2 von 5“ bzw. „zwei Fünftel“.
Bruch (3/9) am Zylinder zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{3}}{\textcolor{#F00}{9}}} \)
Wir wissen, dass der Zylinder in 9 gleich große Stücke zerlegt werden muss. Hierzu zeichnen wir einen senkrechten Zylinder, messen die Höhe und teilen diese durch 9. Diesen Abstandswert tragen wir schrittweise ab und zeichnen die waagerechten Linien. So entstehen 9 Teile am Zylinder. Danach färben wir 3 beliebige Stücke ein.
Wir sprechen „3 von 9“ bzw. „drei Neuntel“.
Bemerkung: \( \frac{3}{9} \) entspricht „1 von 3“ und ist als gekürzter Bruch damit \( \frac{1}{3} \).
Bruch (1/8) am Quader zeichnen
Unser Bruch lautet: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{8}}} \)
Wir wissen, dass der Quader in 8 gleich große Stücke zerlegt werden muss. Hierzu gibt es mehrere Möglichkeiten. Sinnvoll ist zum Beispiel die Einteilung 4 · 2. Wir zeichnen einen Quader, messen die Breite und teilen diese in 4 gleiche Abstände. Danach messen wir die Länge und teilen sie in 2 gleich große Abstände. So entstehen 8 Stücke. Danach färben wir 1 beliebiges Stück ein.
Wir sprechen „1 von 8“ bzw. „ein Achtel“.