Nachstehend eine Übersicht über alle wesentlichen Regeln zum Rechnen mit Brüchen.
1. Bestandteile des Bruches
Ein Bruch ist eine nicht aufgelöste Division (1:2 = \( \frac{1}{2} \)) und besteht aus Zähler, Bruchstrich, Nenner:
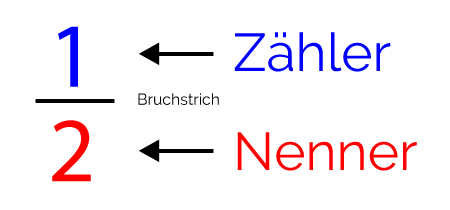
Ein Bruch wird im Gegensatz zu den ganzen Zahlen als „gebrochene Zahl“ bezeichnet.
2. Brüche erweitern
Beim Erweitern von Brüchen werden Nenner und Zähler mit der gleichen Zahl multipliziert:
$$ \frac{2}{5} = \frac{2\textcolor{blue}{·3}}{5\textcolor{blue}{·3}} = \frac{6}{15} $$
Der Wert bleibt gleich. Für das Beispiel 2:5 = 6:15 = 0,4
3. Brüche kürzen
Beim Kürzen von Brüchen werden Nenner und Zähler mit der gleichen Zahl dividiert:
$$ \frac{24}{30} = \frac{24\textcolor{blue}{:6}}{30\textcolor{blue}{:6}} = \frac{4}{5} $$
Der Wert bleibt gleich. Für das Beispiel 24:30 = 4:5 = 0,8.
4. Gleichnamig und ungleichnamig
Wenn die Brüche die gleichen Nenner haben, sagen wir „gleichnamig“.
Beispiel: \( \frac{1}{4}, \frac{3}{4}, \frac{7}{4} \)
Wenn die Brüche unterschiedliche Nenner haben, sagen wir „ungleichnamig“.
Beispiel: \( \frac{1}{2}, \frac{3}{5}, \frac{1}{100} \)
5. Brüche addieren
Bei gleichnamigen Brüchen können wir direkt die Zähler addieren. Der Nenner bleibt auch beim Ergebnis gleich:
$$ \frac{1}{5} + \frac{3}{5} = \frac{1+3}{5} = \frac{4}{5} $$
Bei ungleichnamigen Brüchen müssen wir zuerst durch Erweitern den gleichen Nenner bilden und können dann addieren:
$$ \frac{1}{5} + \frac{1}{8} = \frac{1 \textcolor{#00F}{·8}}{5\textcolor{#00F}{·8}} + \frac{1\textcolor{#F00}{·5}}{8\textcolor{#F00}{·5}} = \frac{8}{40} + \frac{5}{40} = \frac{8+5}{40} = \frac{13}{40} $$
Mehr Information hier: Brüche addieren
6. Brüche subtrahieren
Bei gleichnamigen Brüchen können wir direkt die Zähler subtrahieren. Der Nenner bleibt auch beim Ergebnis gleich:
$$ \frac{4}{7} - \frac{1}{7} = \frac{4-1}{7} = \frac{3}{7} $$
Bei ungleichnamigen Brüchen müssen wir zuerst durch Erweitern den gleichen Nenner bilden und können dann subtrahieren:
$$ \frac{3}{7} - \frac{1}{8} = \frac{3 \textcolor{#00F}{·8}}{7\textcolor{#00F}{·8}} - \frac{1\textcolor{#F00}{·7}}{8\textcolor{#F00}{·7}} = \frac{24}{56} - \frac{7}{56} = \frac{24-7}{56} = \frac{17}{56} $$
Mehr Information hier: Brüche subtrahieren
7. Brüche multiplizieren
Brüche multiplizieren wir, indem wir die Zähler miteinander und die Nenner miteinander multiplizieren:
$$ \frac{1}{6} · \frac{3}{10} = \frac{1·3}{6·10} = \frac{3}{60} $$
Kürzen wir noch das Ergebnis: \( \frac{3}{60} = \frac{3 \textcolor{#00F}{:3}}{60 \textcolor{#00F}{:3}} = \frac{1}{20} \)
Multiplizieren wir einen Bruch mit einer ganzen Zahl, so wandeln wir die ganze Zahl vorher in einen Bruch um:
$$ 7 · \frac{3}{5} = \frac{7}{1} · \frac{3}{5} = \frac{7 · 3}{1 · 5}=\frac{21}{5} $$
8. Brüche dividieren
Brüche dividieren wir, indem wir den Kehrwert des Divisors (der zweite Bruch) bilden und danach die Zähler und Nenner miteinander multiplizieren:
$$ \frac{1}{2} : \frac{\textcolor{#00F}{3}}{\textcolor{#F00}{5}} = \frac{1}{2} · \frac{\textcolor{#F00}{5}}{\textcolor{#00F}{3}} = \frac{1·5}{2·3} = \frac{5}{6} $$
9. Doppelbrüche
Bei einem Doppelbruch ist der Zähler und/oder der Nenner ein Bruch. Beispiel:
$$ \frac{ 7 }{ \frac{2}{3} } = 7 : \frac{2}{3} = 7 · \frac{3}{2} = \frac{7·3}{2} $$
