Beim Kürzen von Brüchen werden Nenner und Zähler mit der gleichen Zahl dividiert, zum Beispiel:
$$ \frac{24}{30} = \frac{24 \textcolor{blue}{ {:} 6}}{30 \textcolor{blue}{ {:} 6}} = \frac{4}{5} $$
Obwohl sich die Zahlen im Nenner und Zähler verändern, bleibt der Wert des Bruches der gleiche!
$$ \frac{24}{30} = \frac{4}{5} = 0,8 $$
Im Beispiel ist der Wert für \( \frac{24}{30} \) und für \( \frac{4}{5} \) jeweils 0,8.
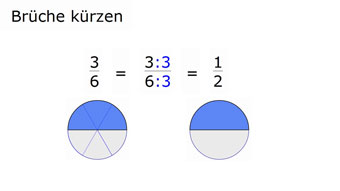
Wir erkennen auch grafisch, dass der Wert (der Anteil) der gleiche bleibt, selbst wenn wir die Stückelung verändern:
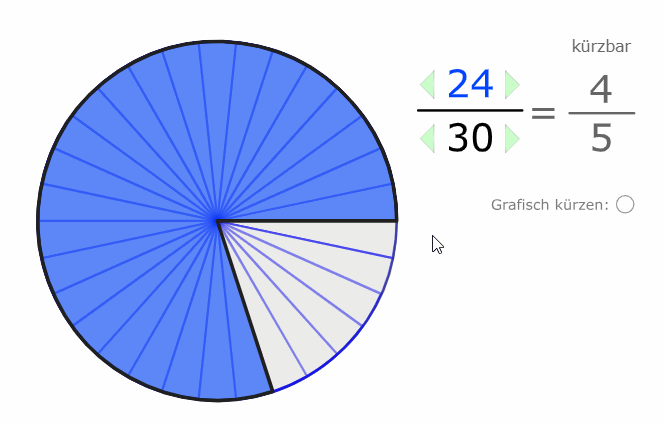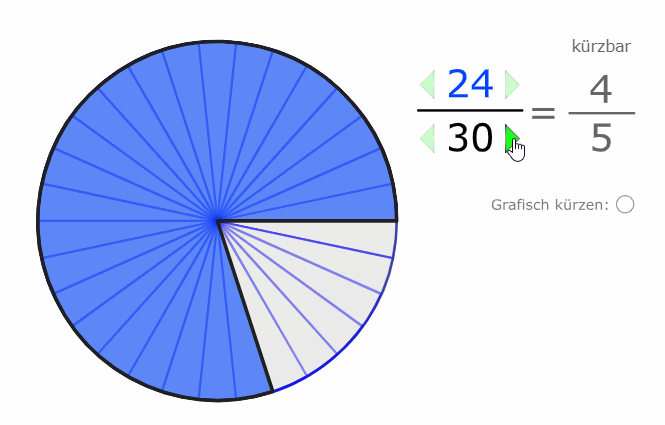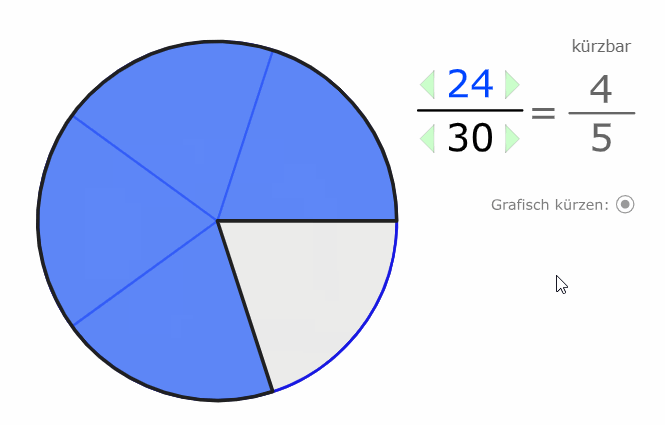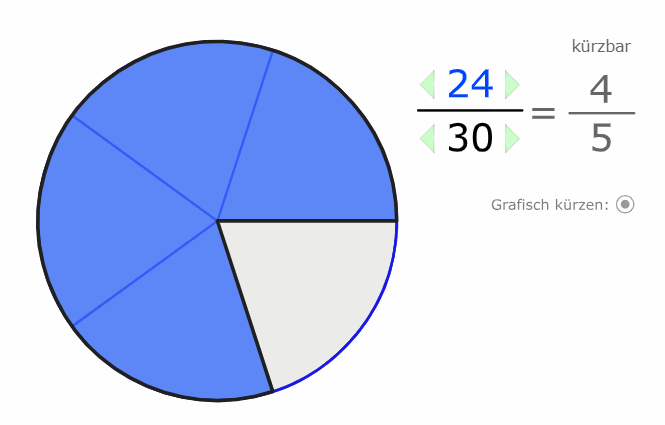
\( \frac{24}{30} \) und \( \frac{4}{5} \) sind beide im Wert 0,8.
Kürzen von Brüchen (Grafik)
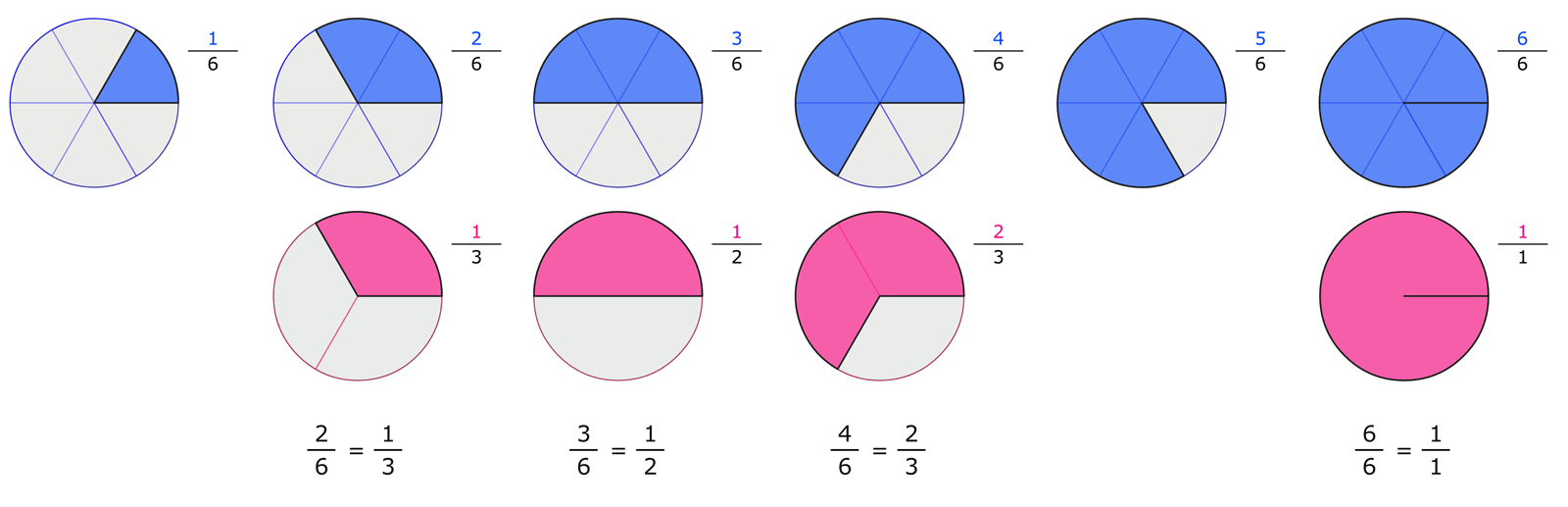
Die folgende Grafik zeigt 6 Brüche (alles Sechstel) und deren Kürzungen. Wir erkennen, dass die Flächen beim gekürzten Bruch stets gleich sind, nur die Stückelungen (Drittel und Halbe) unterscheiden sich.