Erweitern von Brüchen
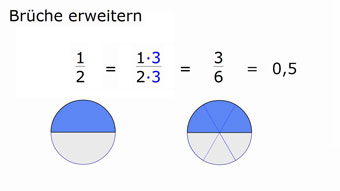
Beim Erweitern von Brüchen werden Zähler und Nenner mit der gleichen Zahl multipliziert, als Beispiel:
$$ \frac{2}{5} = \frac{2\textcolor{blue}{ {·} 3}}{5\textcolor{blue}{ {·} 3}} = \frac{6}{15} $$
Trotzdem sich die Zahlen im Zähler und Nenner verändern, bleibt der Wert des Bruches der gleiche!
$$ \frac{2}{5} = \frac{6}{15} = 0,4 $$
Im Beispiel ist der Wert für \( \frac{2}{5} \) und für \( \frac{6}{15} \) jeweils 0,4.
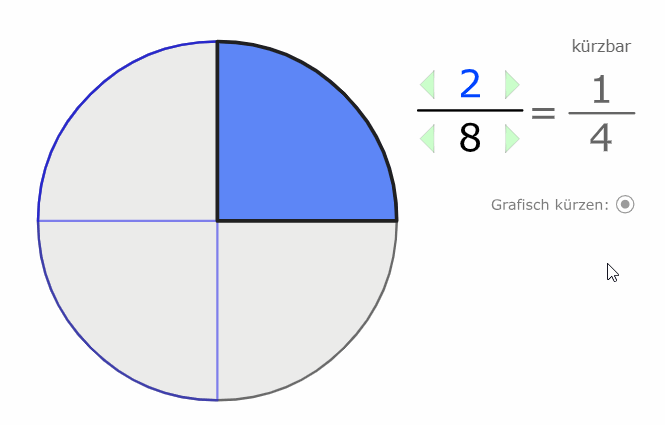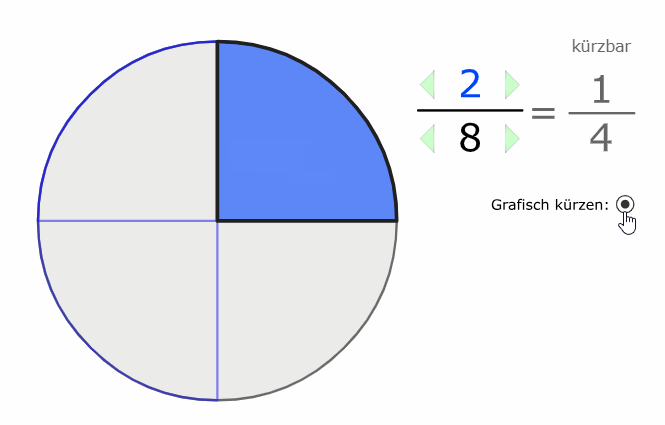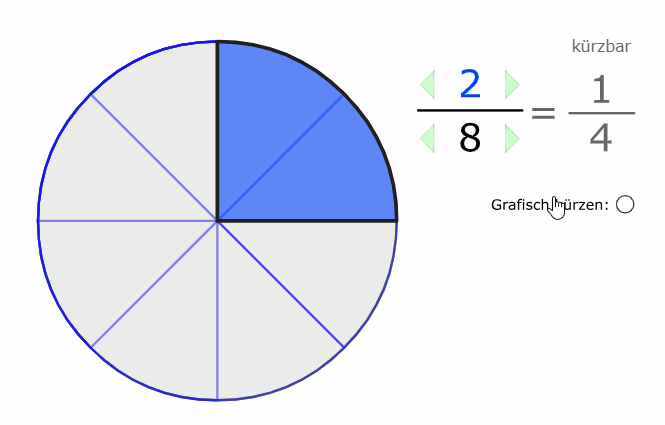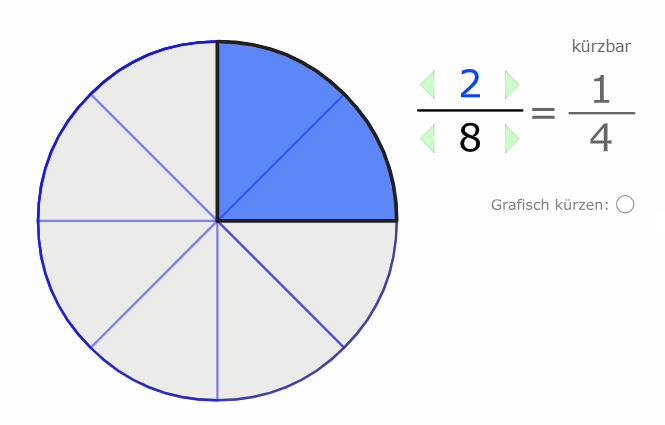
Wir erkennen auch grafisch, dass der Wert (der Anteil) der gleiche bleibt, selbst wenn wir die Stückelung verändern:
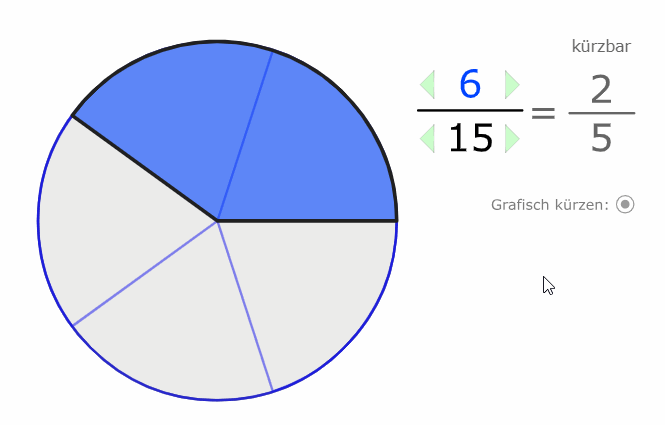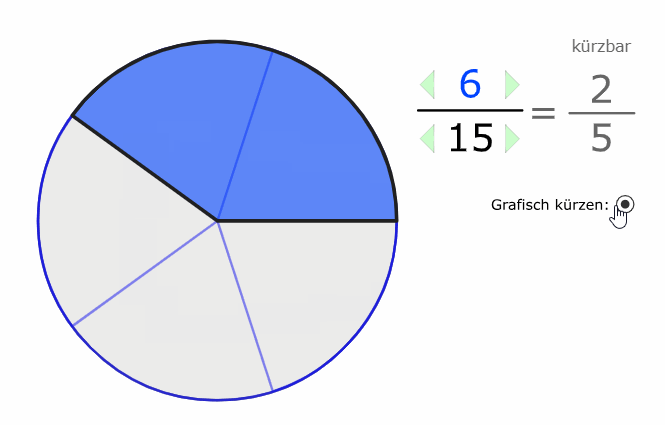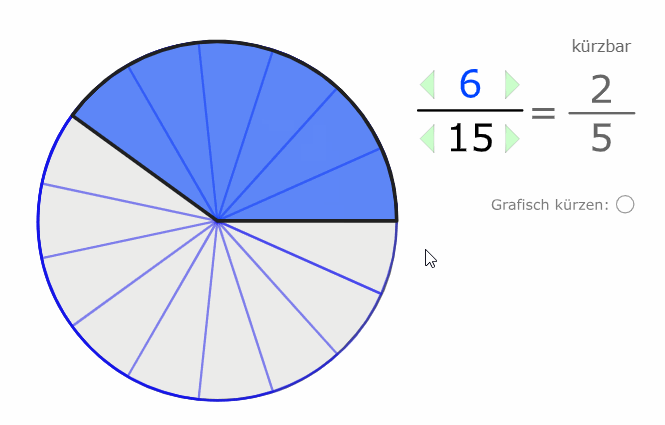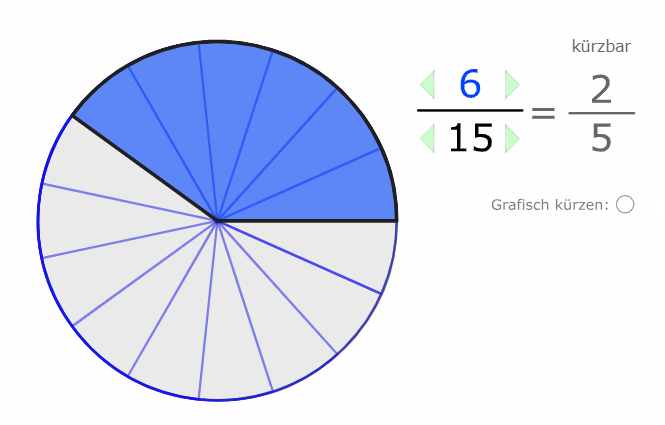
\( \frac{2}{5} \) und \( \frac{6}{15} \) sind beide im Wert 0,4.
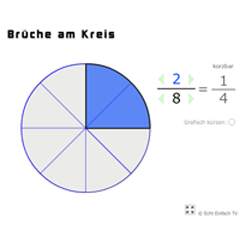
Nachfolgend ein weiteres Beispiel, das zeigt, dass \( \frac{1}{4} \) im Wert das gleiche ist wie \( \frac{2}{8} \), beide Brüche haben den Wert 0,25.
Übungsmaterial: