Brüche lassen sich an einem Zahlenstrahl abtragen. Das heißt, wir setzen einen Strich dort, wo sich der Wert des Bruches als Kommazahl befindet.
Wir hatten uns bereits die echten Brüche am Zahlenstrahl angeschaut. Nun betrachten wir die unechten Brüche, also die Brüche, bei denen der Zähler größer ist als der Nenner, zum Beispiel \( \frac{4}{3} \).
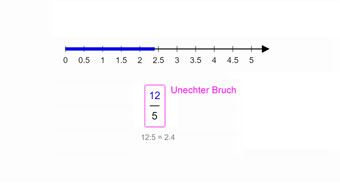
Um unechte Brüche einzeichnen zu können, müssen wir einen Zahlenstrahl wählen, der nicht nur zwischen 0 und 1 groß ist, sondern beliebig größer, denn die Werte von unechten Brüchen sind stets größer als 1, zum Beispiel: \( \frac{12}{5} = 12:5 = 2,4 \).
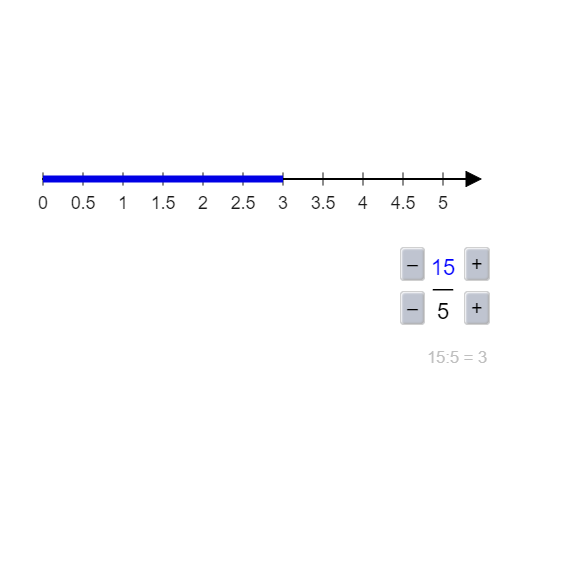
Stelle einen beliebigen (unechten) Bruch ein:
-
Ist der Wert des Bruches zwischen 0 und 1, so handelt es sich um einen echten Bruch.
Beispiel: \( \frac{1}{4} = 0,25 \) und 0,25 liegt zwischen 0 und 1. Wir schreiben: 0 < 0,25 < 1. -
Ist der Wert des Bruches eine ganze Zahl, so ist es ein Scheinbruch.
Beispiel 1: \( \frac{3}{3} = 1 \) und 1 ist eine ganze Zahl.
Beispiel 2: \( \frac{15}{3} = 5 \) und 5 ist eine ganze Zahl. -
Ist der Wert des Bruches größer als 1, so ist es ein unechter Bruch.
Beispiel: \( \frac{10}{4} = 2,5 \) und 2,5 ist größer als 1. Wir schreiben: 2,5 > 1.