Addition von Brüchen
Bei gleichnamigen Brüchen (Brüche mit gleichen Nennern) können wir direkt die Zähler addieren. Der Nenner bleibt auch beim Ergebnis gleich:
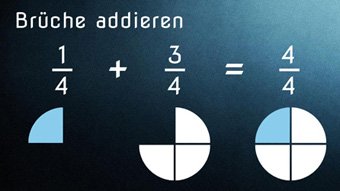
$$ \frac{1}{5} + \frac{3}{5} = \frac{1+3}{5} = \frac{4}{5} $$
Bei ungleichnamigen Brüchen (ungleiche Nenner) müssen wir zuerst durch Erweitern den gleichen Nenner bilden und können dann addieren:
$$ \frac{1}{5} + \frac{1}{8} = \frac{1 \textcolor{#00F}{·8}}{5\textcolor{#00F}{·8}} + \frac{1\textcolor{#F00}{·5}}{8\textcolor{#F00}{·5}} = \frac{8}{40} + \frac{5}{40} = \frac{8+5}{40} = \frac{13}{40} $$
„Gleichnamig machen“ bedeutet, den gleichen Nenner bei den Brüchen zu bilden.
Allgemein:
$$ \frac{a}{\textcolor{red}{b}} + \frac{c}{\textcolor{blue}{d}} = \frac{a\textcolor{blue}{·d}}{b\textcolor{blue}{·d}} + \frac{c\textcolor{red}{·b}}{d\textcolor{red}{·b}} = \frac{a·d + c·b}{\textcolor{red}{b}·\textcolor{blue}{d}} $$
Bei ungleichnamigen Brüchen erweitern wir also den ersten Bruch \( \frac{a}{b} \) mit dem Nenner d vom zweiten Bruch, es entsteht \( \frac{a·d}{b·d} \). Den zweiten Bruch \( \frac{c}{d} \) erweitern wir mit dem Nenner b vom ersten Bruch.
Weiteres Beispiel zur Bruchaddition:
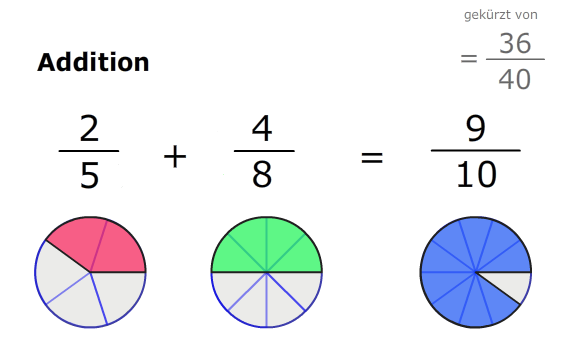
$$ \frac{2}{\textcolor{red}{5}} + \frac{4}{\textcolor{blue}{8}} = \frac{2\textcolor{blue}{·8}}{5\textcolor{blue}{·8}} + \frac{4\textcolor{red}{·5}}{8\textcolor{red}{·5}} = \frac{2·8 + 4·5}{\textcolor{red}{5}·\textcolor{blue}{8}} \\ \space \\ \frac{2·8+4·5}{5·8} = \frac{16+20}{40} = \frac{36}{40} = 0,9 $$
Betrachten wir uns einmal die Dezimalwerte der Rechnung:
$$ \frac{2}{5} + \frac{4}{8} = 2:5 + 4:8 = 0,4 + 0,5 = 0,9 $$
Hauptnenner
Sind beide Brüche voll gekürzt und erschaffen wir einen gemeinsamen Nenner, so nennen wir diesen dann Hauptnenner. Wir ermitteln ihn über das kleinste gemeinsame Vielfache (bzw. mittels Multiplikation beider Nenner).
Beispiel:
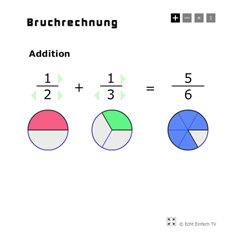
$$ \frac{1}{2} + \frac{1}{3} = \frac{1·3}{2·3} + \frac{1·2}{3·2} = \frac{3}{\textcolor{#00F}{6}} + \frac{2}{\textcolor{#00F}{6}} = \frac{3+2}{\textcolor{#00F}{6}} = \frac{5}{\textcolor{#00F}{6}} $$
Addition von Brüchen (grafisch)
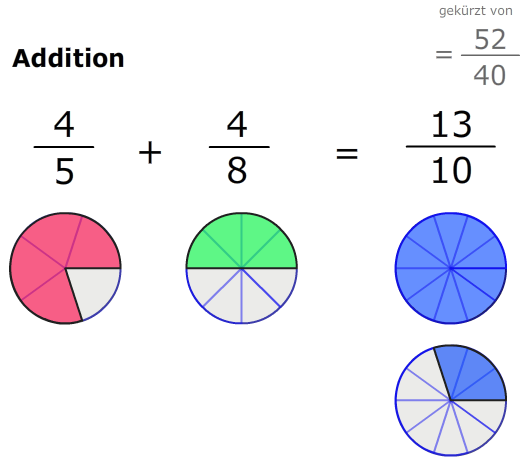
Die Addition von Brüchen kann grafisch sehr anschaulich dargestellt werden. Man legt die Stücke einfach zusammen:
Wenn bei der Addition ein Ergebnis größer als 1 herauskommt, z. B. \( \frac{13}{10} = 1,3 \) als Dezimalzahl, so erhält man grafisch 1 kompletten Kreis und zusätzlich einen Kreis, der zu 0,3 gefüllt ist: