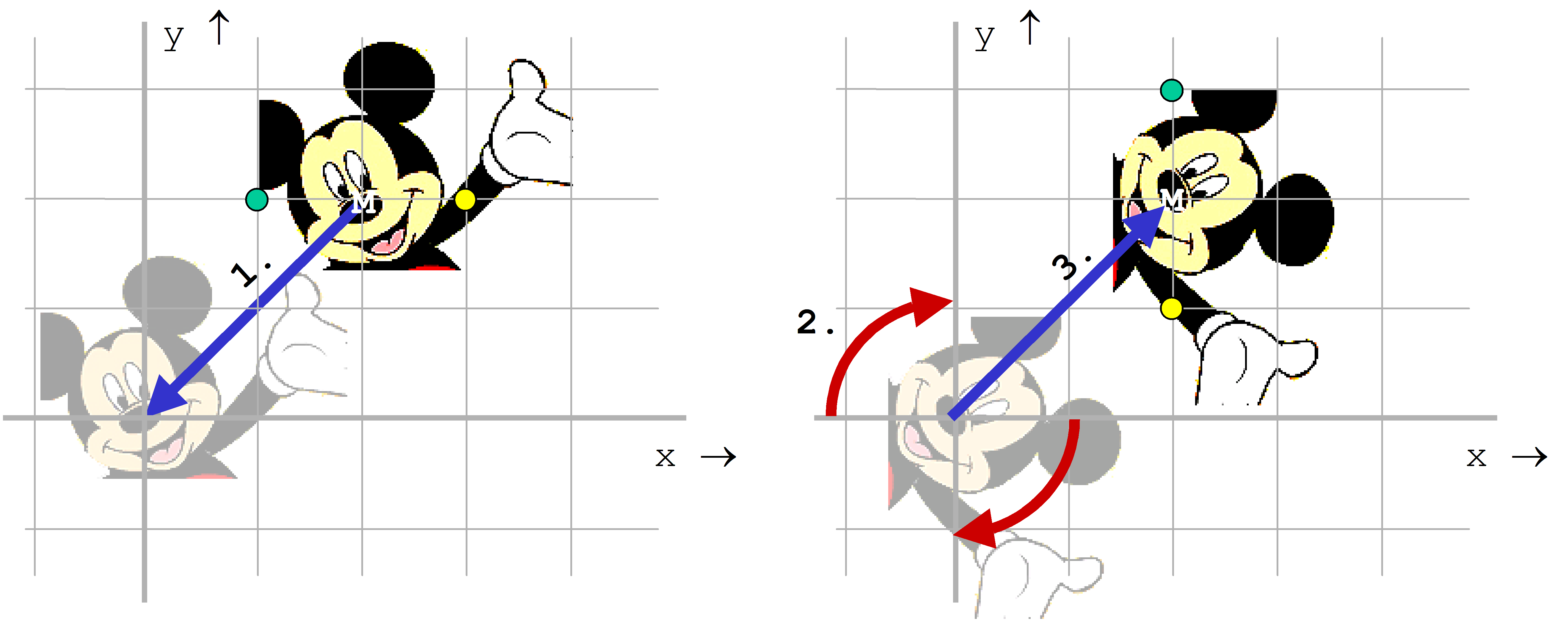
Bestimmte Aufgaben machen die Umkehrung von Transformationsschritten (siehe Ähnlichkeitstransformation 4.6.2 e) notwendig. Dies ist zum Beispiel der Fall, wenn ein Objekt, das sich nicht im Ursprung befindet, nur um sich selbst rotiert werden soll. Damit keine Positionsveränderung des Objektes bei der Rotation erfolgt, wird die Rotation um sich selbst in drei Schritten vorgenommen. Im ersten Schritt wird das Objekt in den Ursprung verschoben, im zweiten rotiert und im dritten Schritt an seinen Ausgangsort zurück verschoben.
Umkehroperationen werden durch die Bildung des Kehrwertes der Ausgangsmatrix ausgeführt. So gelten für die
Translation:
\( T = \left( { \begin{array}{cc}1&0&{ {t_x} }\\0&1&{ {t_y} }\\0&0&1\end{array} } \right) \quad \Rightarrow \quad {T^{ - 1} } = \left( { \begin{array}{cc} 1&0&{ - {t_x} } \\ 0&1&{ -{t_y} } \\ 0&0&1\end{array} } \right) \) Gl. 232
Skalierung:
\( S = \left( {\begin{array}{cc} { {s_x} }&0&0 \\ 0&{ {s_y} }&0 \\ 0&0&1\end{array} } \right) \quad \Rightarrow \quad {S^{ - 1} } = \left( {\begin{array}{cc} \frac{1}{s_x} & 0 & 0 \\ 0 & \frac{1}{s_y} & 0 \\ 0 & 0 & 1 \end{array} } \right) \) Gl. 233
Scherung:
Nach Gl. 199 (Inverse Matrix) wird die Kehrwertbildung wie folgt ausgeführt:
\(S{h^{ - 1} } = {\left( {\begin{array}{cc}1&{ {a_x} }&0\\{ {a_y} }&1&0\\0&0&1\end{array} } \right)^{ - 1} } = \frac{1}{ {\det (Sh)} } \cdot {\left( {\begin{array}{cc}{ {A_{11} } }&{ {A_{12} } }&{ {A_{13} } }\\{ {A_{21} } }&{ {A_{22} } }&{ {A_{23} } }\\{ {A_{31} } }&{ {A_{32} } }&{ {A_{33} } }\end{array} } \right)^T}\) Gl. 234
wobei
\(\det (sh) = 1 \cdot \left| {\begin{array}{cc}1&{ {a_x} }\\{ {a_y} }&1\end{array} } \right| = 1 - {a_x} \cdot {a_y}\) und
\(\left( {\begin{array}{cc}{ {A_{11} } }&{ {A_{12} } }&{ {A_{13} } }\\{ {A_{21} } }&{ {A_{22} } }&{ {A_{23} } }\\{ {A_{31} } }&{ {A_{32} } }&{ {A_{33} } }\end{array} } \right) = \left( {\begin{array}{cc}1&{ - {a_y} }&0\\{ - {a_x} }&1&0\\0&0&{1 - {a_x}{a_y} }\end{array} } \right)\) damit
\( Sh = \left( {\begin{array}{cc}1&{ {a_x} }&0\\{ {a_y} }&1&0\\0&0&1\end{array} } \right) \quad \Rightarrow \quad S{h^{ - 1} } = \frac{1}{ {1 - {a_x}{a_y} } } \cdot \left( { \begin{array}{cc} 1&{ - {a_x} }&0 \\ {-{a_y} }&1&0 \\ 0&0&{1 - {a_x}{a_y} } \end{array} } \right) \) Gl. 235
Rotation:
\( R = \left( {\begin{array}{cc}{\cos \phi }&{ - \sin \phi }&0\\{\sin \phi }&{\cos \phi }&0\\0&0&1\end{array} } \right) \quad \Rightarrow \quad { R^{-1} } = \left( { -\begin{array}{cc} {\cos \phi }&{\sin \phi }&0 \\ {\sin \phi }&{\cos \phi }&0 \\ 0&0&1 \end{array} } \right) \) Gl. 236
Beispiel:
Gegeben seien die Punkte P1(1;2) und P2(3;2) eines Objektes, das um einen Winkel von -90° (also im Uhrzeigersinn) um seinen Mittelpunkt zu rotieren ist. Der Mittelpunkt des Objektes liegt im Punkt PM(2;2).
Lösung:
Zunächst sind die Punkte P1 und P2 so zu verschieben, dass der Mittelpunkt des Objektes in den Ursprung verlegt wird:
\(T = \left( {\begin{array}{cc}1&0&{ - 2}\\0&1&{ - 2}\\0&0&1\end{array} } \right)\)
dann kann die Rotation um 90° erfolgen
\(R \cdot T = \left( {\begin{array}{cc}0&1&0\\{ - 1}&0&0\\0&0&1\end{array} } \right) \cdot \left( {\begin{array}{cc}1&0&{ - 2}\\0&1&{ - 2}\\0&0&1\end{array} } \right)\)
schließlich wird das Objekt an seinen ursprünglichen Ort zurück verschoben:
\({T^{ - 1} } \cdot R \cdot T = \left( {\begin{array}{cc}1&0&2\\0&1&2\\0&0&1\end{array} } \right) \cdot \left( {\begin{array}{cc}0&1&0\\{ - 1}&0&0\\0&0&1\end{array} } \right) \cdot \left( {\begin{array}{cc}1&0&{ - 2}\\0&1&{ - 2}\\0&0&1\end{array} } \right) = \left( {\begin{array}{cc}0&1&0\\{ - 1}&0&4\\0&0&1\end{array} } \right)\)
Daraus folgen nunmehr die neuen Koordinaten der gesuchten Punkte:
\(P1' = {T^{ - 1} } \cdot R \cdot T \cdot P1 = \left( {\begin{array}{cc}0&1&0\\{ - 1}&0&4\\0&0&1\end{array} } \right) \cdot \left( {\begin{array}{cc}1\\2\\1\end{array} } \right) = \left( {\begin{array}{cc}2\\3\\1\end{array} } \right)\) und \(P2' = {T^{ - 1} } \cdot R \cdot T \cdot P2 = \left( {\begin{array}{cc}0&1&0\\{ - 1}&0&4\\0&0&1\end{array} } \right) \cdot \left( {\begin{array}{cc}3\\2\\1\end{array} } \right) = \left( {\begin{array}{cc}2\\1\\1\end{array} } \right)\)