In der Physik hat das Skalarprodukt u.a. die Aufgabe, die geleistete Arbeit längs eines vorgegebenen Weges zu berechnen. Die geleistete Arbeit ergibt sich aus dem Produkt von aufgewendeter Kraft F und zurückgelegtem Weg s, wenn beide Größen parallel zueinander ausgerichtet sind. Ist dies nicht der Fall, wirken nur die Komponenten, die parallel zueinander liegen. Das ist gleichbedeutend damit, dass die jeweiligen Richtungskomponenten der Kraft und des Weges miteinander multipliziert und diese Teilprodukte schließlich addiert werden (Abbildung 38):

\( W = \vec F \cdot \vec s = {F_x} \cdot {s_x} + {F_y} \cdot {s_y} + {F_z} \cdot {s_z} \) Gl. 305
Wobei das Skalarprodukt auch durch die Beträge der Vektoren und den Cosinus des von beiden Vektoren eingeschlossenen Winkels definiert ist.
Anders ausgedrückt, es werden nur die Komponenten der Vektoren multipliziert, die parallel zu einander sind (Abbildung 39):
\( W = \left| {\vec F} \right| \cdot \left| {\vec s} \right| \cdot \cos \left( {\angle \vec F,\vec s} \right) \) Gl. 306
Entsprechend Gl. 305 kann das Skalarprodukt auch als Matrizenprodukt ausgedrückt werden. Dabei sind jedoch die Rechenregeln für Matrizenprodukte zu beachten:
\( W = {F^T} \cdot S = \left( {\begin{array}{cc}{ {F_x} }&{ {F_y} }&{ {F_z} }\end{array} } \right) \cdot \left( {\begin{array}{cc}{ {s_x} }\\{ {s_y} }\\{ {s_z} }\end{array} } \right) \) Gl. 307
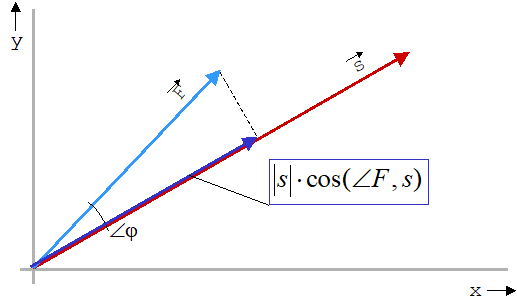
Da das Ergebnis Energie eine ungerichtete Größe, also ein Skalar, ist, wird dieses Produkt auch Skalarprodukt genannt.
Die Definition des Skalarproduktes (Gl. 306) kann u.a. zur Bestimmung des Winkels zwischen zwei Vektoren benutzt werden. Umstellen von Gl. 306 nach dem Winkel ergibt
\( \cos \left( {\angle \vec a,\vec b} \right) = \frac{ {\left| {\vec a \cdot \vec b} \right|} }{ {\left| {\vec a} \right| \cdot \left| {\vec b} \right|} } \) Gl. 308
Beispiel:
Gegeben seien die Punkte P1(3,4) und P2(4,2) in der x-y-Ebene. Gesucht ist der Winkel zwischen den beiden Ortsvektoren, die zu diesen Punkten gehören.
Mit \(\vec a = 3i + 4j\) und \(\vec b = 4i + 2j\) folgt
\( \cos \left( {\angle \vec a,\vec b} \right) = \frac{ {\left| {\vec a \cdot \vec b} \right|} }{ {\left| {\vec a} \right| \cdot \left| {\vec b} \right|} } = \frac{ {3 \cdot 4 + 4 \cdot 2} }{ {\sqrt { {3^2} + {4^2} } \cdot \sqrt { {4^2} + {2^2} } } } = \frac{ {20} }{ {5 \cdot \sqrt {20} } } = 0,8944... \)
\( \angle \vec a,\vec b = \arccos \left( {0,8944...} \right) = {26,56^o} \)
Rechenregeln für Skalarprodukte
Es gelten das
- Kommutativgesetz
\(\vec a \cdot \vec b = \vec b \cdot \vec a \) Gl. 309
und das
- Assoziativgesetz für zwei Vektoren und einen Skalar
\( \lambda \cdot \left( {\vec a \cdot \vec b} \right) = \left( {\lambda \cdot \vec a} \right) \cdot \vec b \) Gl. 310
· das Assoziativgesetz gilt hingegen nicht für drei und mehr Vektoren
\( \left( {\vec a \cdot \vec b} \right) \cdot \vec c \ne \vec a \cdot \left( {\vec b \cdot \vec c} \right) \) Gl. 311
- das Distributivgesetz gilt
\( \vec a \cdot \left( {\vec b \pm \vec c} \right) = \vec a \cdot \vec b \pm \vec a \cdot \vec c \) Gl. 312
Eigenschaften des Skalarproduktes
a) Das Skalarprodukt zwei gleicher Vektoren ergibt das Betragsquadrat dieses Vektors.
b) Stehen zwei Vektoren senkrecht zueinander, so beträgt der von ihnen eingeschlossene Winkel 90°. Folglich verschwindet das Skalarprodukt zueinander senkrechter Vektoren.
\( \vec a \cdot \vec b = 0 \quad \text{ sofern } a \bot b \) Gl. 313
Wenn ausgeschlossen werden kann, dass \(\vec a,\,\vec b \ne 0\) sind, kann dieses Verhalten zur Prüfung der Orthogonalität zweier Vektoren verwendet werden.
Beispiel:
Gegeben sind die Vektoren \(\vec a = \left( {\begin{array}{cc}2\\3\\{ - 4}\end{array} } \right)\)und \(\vec b = \left( {\begin{array}{cc}4\\0\\2\end{array} } \right)\). Es ist zu prüfen, ob die Vektoren senkrecht zueinander stehen.
Die Skalarmultiplikation ergibt
\({A^T} \cdot B = \left( {\begin{array}{cc}2&3&{ - 4}\end{array} } \right) \cdot \left( {\begin{array}{cc}4\\0\\2\end{array} } \right) = 8 + 0 - 8 = 0\)
also sind beide Vektoren senkrecht zueinander.
