In der Physik hat das Vektorprodukt (auch Kreuzprodukt genannt) z.B. die Aufgabe, das Drehmoment an einem Hebelarm der Länge s, an dem eine Kraft F angreift, zu ermitteln. Das Drehmoment ergibt sich aus dem Produkt von angreifender Hebellänge s und Kraft F, wenn beide Größen rechtwinklig zueinander ausgerichtet sind (z. B. Kurbelantrieb am Fahrrad). Ist dies nicht der Fall, wirken nur die Komponenten, die in einem rechten Winkel zueinander stehen.
Im Gegensatz zum Skalarprodukt, ist das Ergebnis des Vektorproduktes wieder ein Vektor!
Weil immer nur rechtwinklig zueinander stehende Komponenten eine Wirkung im Sinne eines Drehmomentes ausüben können, werden auch nur diese vorzeichenrichtig miteinander verknüpft. Abbildung 40 zeigt dies an einem zweidimensionalen Beispiel.
Die Vektoren von Kraft und Hebelarm werden in ihre Komponenten zerlegt. Nur die rechwinklig zueinander stehenden Komponenten (parallele Komponenten liefern ja keinen Beitrag!) werden miteinander multipliziert und die Produkte vorzeichenrichtig zusammengefasst:
\( \vec M = \vec s \times \vec F = \left( { {s_x}{F_y} - {s_y}{F_x} } \right) · k \) Gl. 314

Der Ergebnisvektors ist so gerichtet, dass er senkrecht auf der durch die beiden Faktoren aufgespannten Fläche steht. Die Orientierung ergibt sich nach der schon bekannten Rechte-Hand-Regel (Abbildung 41).
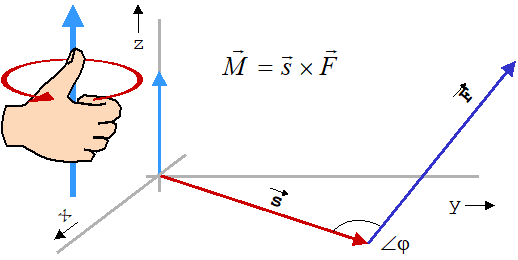
Im dreidimensionalen Fall erfolgt die Multiplikation so, dass sich immer die beteiligten Richtungskomponenten zu genau der Richtung ergänzen, zu der beide senkrecht stehen:
\( \vec M = \vec s \times \vec F = \left( { {F_z}{s_y} - {F_y}{s_z} } \right) \cdot i + \left( { {F_x}{s_z} - {F_z}{s_x} } \right) \cdot j + \left( { {F_y}{s_x} - {F_x}{s_y} } \right) \cdot k \) Gl. 315
Da die Berechnungsvorschrift für das Kreuzprodukt wenig anschaulich ist, gibt es eine auf der Determinantenschreibweise fußende Form:
\( \vec s \times \vec F = \left| {\begin{array}{cc}i&j&k\\{ {s_x} }&{ {s_y} }&{ {s_z} }\\{ {F_x} }&{ {F_y} }&{ {F_z} }\end{array} } \right| = \left( { {F_z}{s_y} - {F_y}{s_z} } \right) \cdot i + \left( { {F_x}{s_z} - {F_z}{s_x} } \right) \cdot j + \left( { {F_y}{s_x} - {F_x}{s_y} } \right) \cdot k \) Gl. 316
Auch eine Matrizendarstellung ist möglich. Jedoch nimmt sie die eigentliche Berechnung des Vektorproduktes vorweg, ist also keine Rechenvorschrift im Sinne der Matrizenrechnung. Allgemein gilt demnach:
\(\vec a \times \vec b = \left| {\begin{array}{cc}i&j&k\\{ {a_x} }&{ {a_y} }&{ {a_z} }\\{ {b_x} }&{ {b_y} }&{ {b_z} }\end{array} } \right| = \left( { {a_y}{b_z} - {a_z}{b_y} } \right) \cdot i + \left( { {a_z}{b_x} - {a_x}{b_z} } \right) \cdot j + \left( { {a_x}{b_y} - {a_y}{b_x} } \right) \cdot k = \left( {\begin{array}{cc}{ {a_y}{b_z} - {a_z}{b_y} }\\{ {a_z}{b_x} - {a_x}{b_z} }\\{ {a_x}{b_y} - {a_y}{b_x} }\end{array} } \right) \) Gl. 317
Andererseits ist das Vektorprodukt der Definition nach auch durch die Beträge der beiden Vektoren und den Sinus des von beiden Vektoren eingeschlossenen Winkels gegeben:
\( \left| {\vec a \times \vec b} \right| = \left| {\vec a} \right| \cdot \left| {\vec b} \right| \cdot \sin \left( {\angle \vec a,\vec b} \right) \) Gl. 318
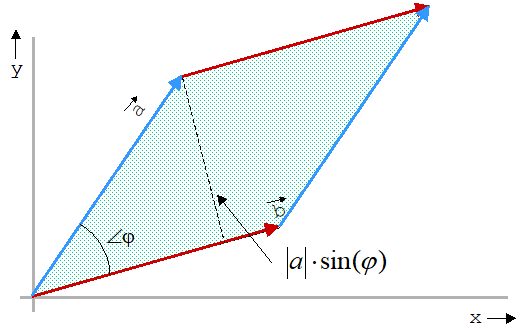
Aus Gl. 318 geht hervor, dass das Vektorprodukt betragsmäßig gleichgroß zu der Fläche des Parallelogramms ist, das die beiden Vektoren aufspannen.
Beispiel:
Gegeben seien die Punkte P1(3,4) und P2(4,2) in der x-y-Ebene. Gesucht ist Fläche zwischen den beiden Ortsvektoren, die zu diesen Punkten gehören.
Beachte: Die gesuchte Fläche ist genau halb so groß wie die Fläche des Parallelogramms, das beide Vektoren aufspannt.
Mit \(\vec a = 3i + 4j\) und \(\vec b = 4i + 2j\) folgt
\(F = \frac{ {\left| {\vec a \times \vec b} \right|} }{2} = \frac{1}{2}\left\| {\begin{array}{cc}i&j&k\\3&4&0\\4&2&0\end{array} } \right\| = \frac{1}{2}\left| {\left( {6 - 16} \right)k} \right| = 5 \; FE \)
